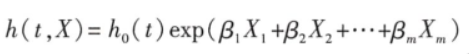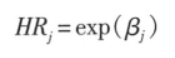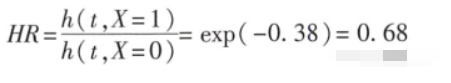一、生存分析的基本概念
- 生存时间:从规定的观察起点至事件终点出现所经历的时间长度。
- 生存数据:① 完全数据:准确的生存时间;② 删失数据/截尾数据:由于某种原因无法观察到事件终点出现的数据。
删失数据的原因包括:1)研究结束时终点事件未发生;2)失访;3)研究对象因其他原因死亡或无法耐受而终止观察。
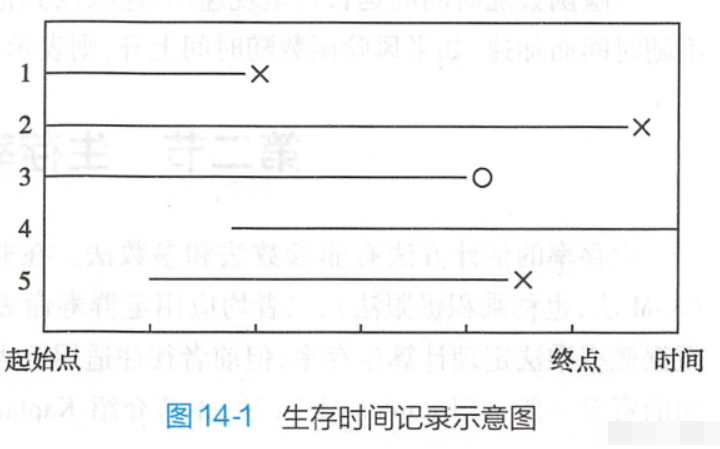
如上图所示:1号和5号 观察期间内患者死亡,为完全数据;
2号在观察结束后死亡、3号失访、4号始终未观察到终点事件,这3个数据为删失数据。
二、 生存分析的常用指标
- 中位生存期(Median survival time):50%个体存活的时间。
- 生存函数(Survival function):某时刻观察对象仍然存活的概率,与时间相关,又称积累生存率。
- 风险函数(Hazard function) :某时刻观察对象的瞬时死亡率。
三、Kaplan-Meier 生存曲线
Kaplan-Meier法,即计算的是上述概念所提到的积累生存率,是一种单因素生存分析方法,可用于研究1个因素对于生存时间的影响。
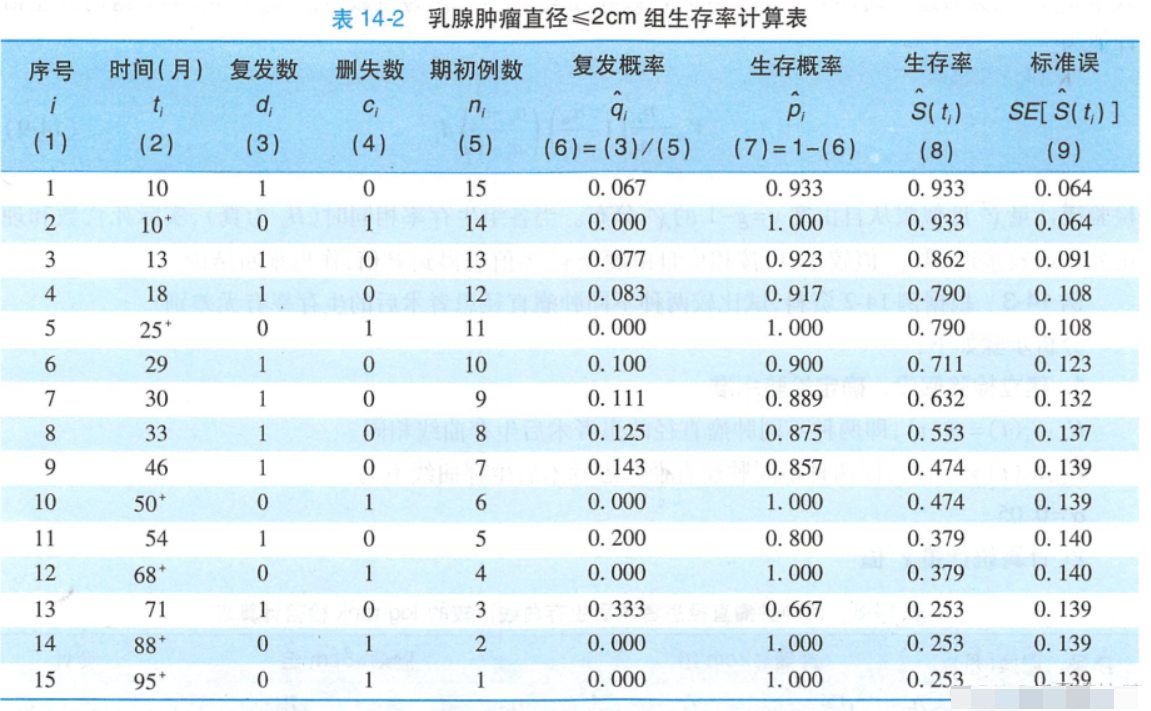

如上图所示:
曲线上的“+”表示删失数据;
曲线越高、下降越平缓表示生存率越高或预后越好;
曲线越低、下降越陡峭表示生存率越低或预后不佳;
蓝色圈表示中位生存期,肿瘤直径>5cm组中位生存期约23月,≤2cm组约45月;
四、生存率的比较
- 单因素分析方法检验
非参数检验方法使用较为广泛,主要包括log-rank检验和Breslow检验,二者都属于卡方检验。
log-rank检验给组间死亡的远期差别更大,即log-rank方法对远期差异敏感。
Breslow检验给组间死亡的近期差别更大,即Breslow方法对近期差异敏感。
当生存曲线有交叉时,提示具有混杂因素的影响,这两种检验方法不适用。此时可以考虑R语言TSHRC包的Two-Stage方法进行检验,可以同时计算Kaplan-Meier和log-rank test的p值。
- 多因素Cox回归模型检验
(1)cox回归模型的基本表达式:
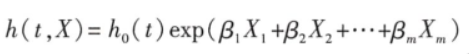
h(t)即风险函数,指在t时刻观察对象的瞬时死亡率;
X1m是自变量,β1m是对应X的回归系数;
因此风险函数展示了多个自变量X对因变量h(t)的影响。
回归系数 β 与 HR (Hazard Ratio) 有对应关系,经过对数转换,自变量X取特殊值:X=0表示未暴露组,X=1表示暴露组,风险函数可以改写为
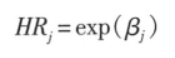
(2)风险比(HR, Hazard Ratio)
【举例】分析乳腺癌术后复发时间与是否化疗有关。X=0表示患者未接受化疗,X=1表示患者接受化疗,经过分析X的回归系数β= -0.38。故HR如下:
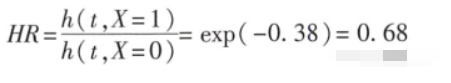
提示接受化疗的乳癌术后患者复发的风险为不接受化疗患者的0.68倍。
五、生存曲线绘制及假设检验
前文所述,对生存分析的基本概念和方法有了基本的认识,现在可以结合之前整理的tcga临床数据来进行生存曲线的绘制。
生存曲线绘制的代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| rm(list = ls()) #### 魔幻操作,一键清空~
getwd()
setwd('C:/Users/Administrator/project_gdc2')
# 加载包,准备绘制KM生存曲线
library(survival)
library(survminer)
library(dplyr)
library(ggplot2)
options(datatable.fread.datatable=FALSE)#保证fread返回数据框
df <- fread('./RawData/03.LIHC_clin.txt')
class(df)
colnames(df)
# 对患者进行分组
a <- select(df,c("month","Race","Gender","Status","Stage","Age","OS")) # 提取分析需要的列
# survdata = Surv(time = month, event = Status =='Dead') # 存储生存数据
a$Age <- factor(cut(a$Age,breaks=c(-Inf,median(a$Age),Inf),
labels = c("Young","Old"))) # 按中位年龄对患者进行分层
sfit <- survfit(Surv(time = month, event = Status == 'Dead') ~ Age, data = a)
sfit
# 进行假设检验
# 两组间的检验可以使用survdiff函数
data.survdiff <- survdiff(Surv(time = month, event = Status =='Dead') ~ Age,data = a)
data.survdiff
# 计算P值
p.val = 1 - pchisq(data.survdiff$chisq, length(data.survdiff$n) - 1)
p.val
# 分组多可以使用pairwise_survdiff函数进行两两检验
# data.survdiff2 <- pairwise_survdiff(Surv(month,Status)~Race,data = a)
# data.survdiff2
# data.survdiff2$p.value
|
绘制简单的生存曲线:
1
2
| plot1 <- ggsurvplot(sfit, data = a)
plot1
|
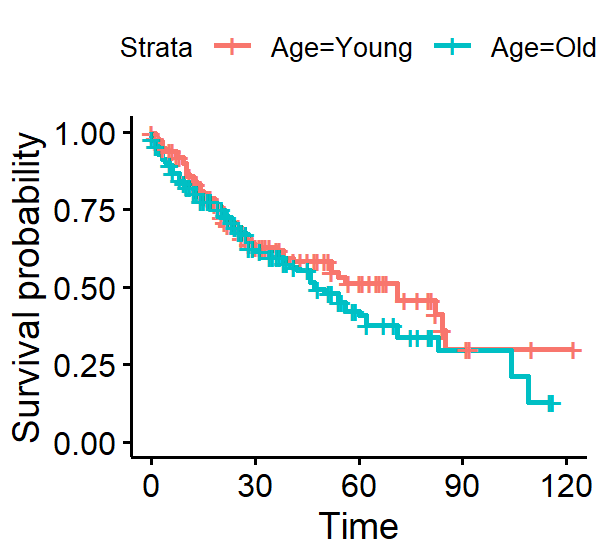
优化生存曲线,添加p值:
1
2
3
4
| plot2 <- ggsurvplot(sfit,
data = a,
pval = T)
plot2
|
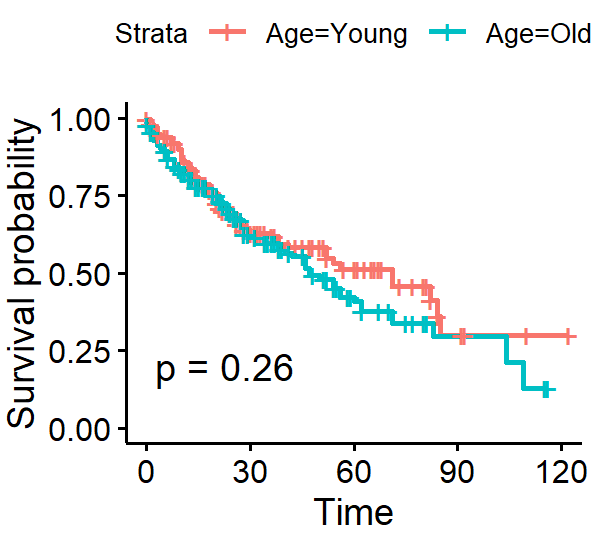
可以看到按中位年龄分组,两组的生存率没有明显的统计学差异,p=0.26
进一步优化生存曲线,添加95%置信区间、风险表等,让图更加美观!
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| plot3 <- ggsurvplot(sfit, # 创建的拟合对象
data = a, # 指定变量数据来源
conf.int = TRUE, # 显示置信区间
pval = TRUE, # 添加P值
surv.median.line = "hv", # 添加中位生存时间线
risk.table = TRUE, # 添加风险表
risk.table.height=.25,
xlab = "Time in months",
ylab = "Overall Survival Probability",
legend = c(0.8,0.75), # 指定图例位置
legend.title = "Age", # 设置图例标题“Age”
legend.labs = c("Young","Old"), # 指定图例分组标签
break.x.by = 20, # 设置x轴刻度间距
palette = "hue") # 默认为hue,可以自定义调色板 "grey","npg","aaas","lancet","jco", "ucscgb","uchicago","simpsons"和"rickandmorty"
plot3
|
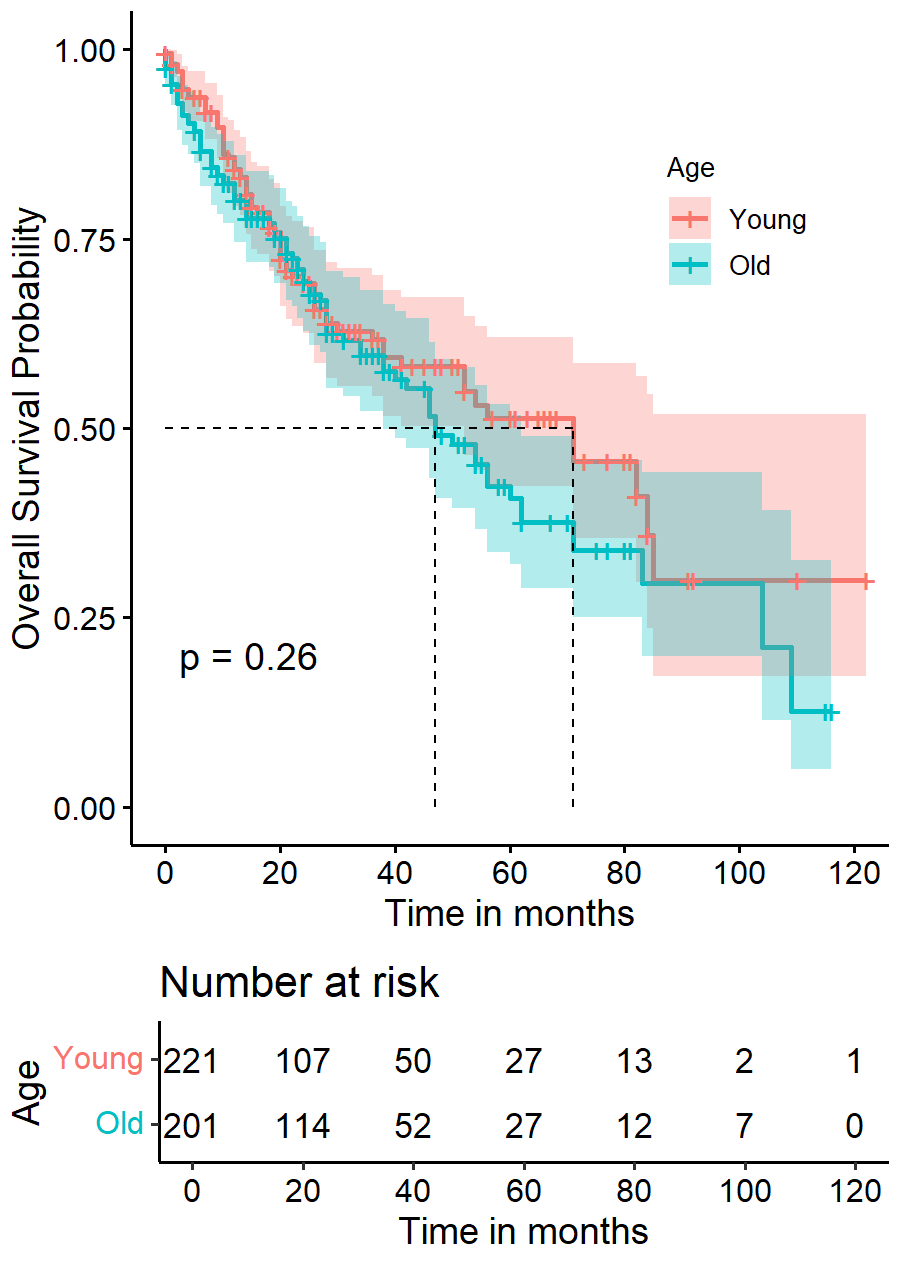
还可以添加总生存曲线:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| plot4 <- ggsurvplot(sfit, # 创建的拟合对象
data = a, # 指定变量数据来源
conf.int = TRUE, # 显示置信区间
pval = TRUE, # 添加P值
surv.median.line = "hv", # 添加中位生存时间线
risk.table = TRUE, # 添加风险表
risk.table.height=.25,
xlab = "Time in months",
ylab = "Overall Survival Probability",
legend = c(0.8,0.75), # 指定图例位置
legend.title = "Age", # 设置图例标题为“Age”
legend.labs = c("All","Young","Old"), # 指定图例分组标签
break.x.by = 20, # 设置x轴刻度间距
palette = "hue", # 默认为hue,可以自定义调色板 "grey","npg","aaas","lancet","jco", "ucscgb","uchicago","simpsons"和"rickandmorty"
add.all = TRUE) # 添加总患者生存曲线
plot4
|
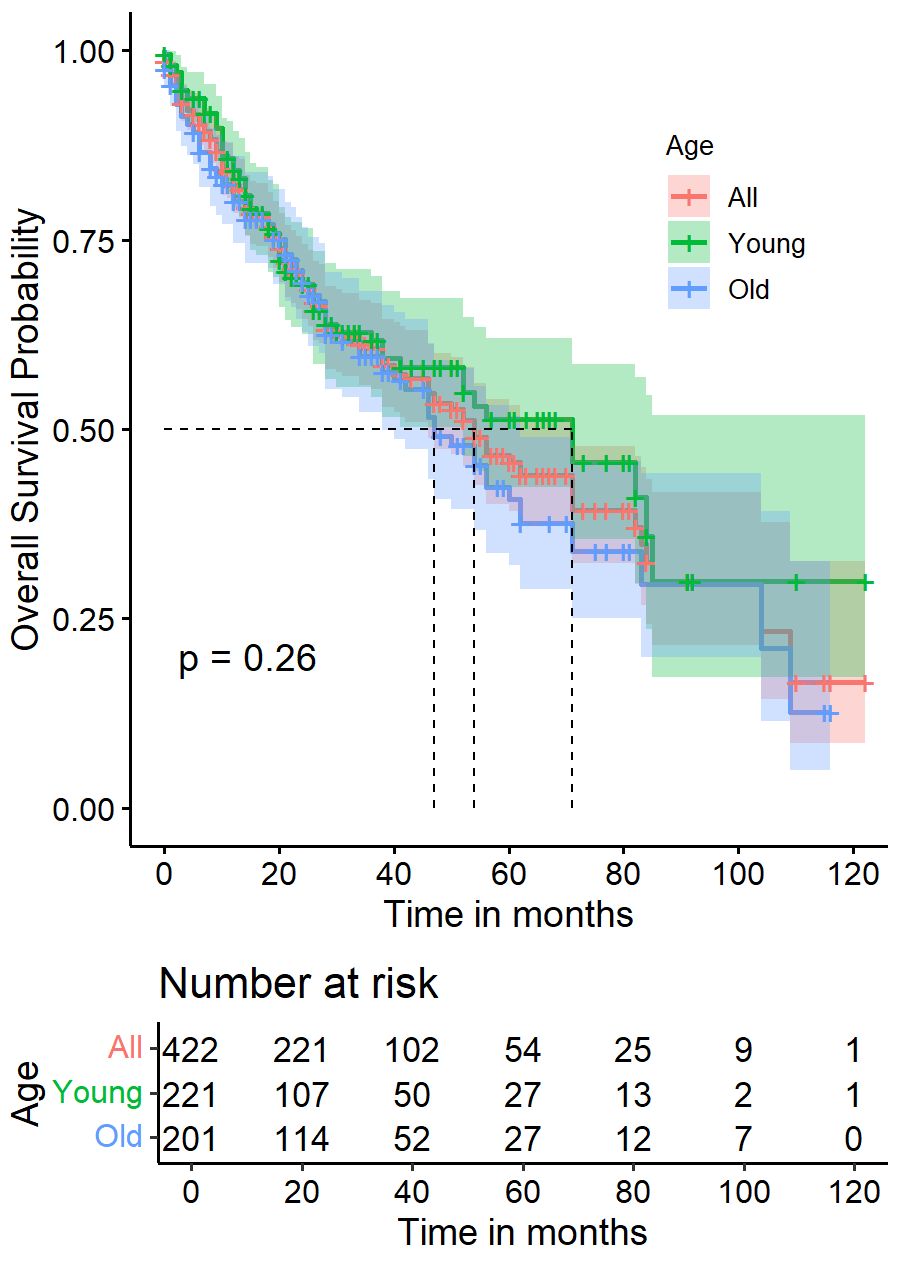
六、Cox回归分析
接下来我们利用cox模型计算HR
1
2
3
4
5
| ### cox回归分析计算HR
b <- select(df,c("month","Race","Gender","Status","Stage","Age","OS"))
res.cox <- coxph(Surv(time = month, event = Status == 'Dead') ~ Age, data = b)
coxSummary <- summary(res.cox)
coxSummary
|
结果:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| > coxSummary
Call:
coxph(formula = Surv(time = month, event = Status == "Dead") ~
Age, data = b)
n= 422, number of events= 164
coef exp(coef) se(coef) z Pr(>|z|)
Age 0.008939 1.008979 0.006062 1.475 0.14
exp(coef) exp(-coef) lower .95 upper .95
Age 1.009 0.9911 0.9971 1.021
Concordance= 0.524 (se = 0.026 )
Likelihood ratio test= 2.25 on 1 df, p=0.1
Wald test = 2.17 on 1 df, p=0.1
Score (logrank) test = 2.18 on 1 df, p=0.1
|
cox分析结果:HR=1.009(1.003-1.015),似然比检验和Wald检验p均大于0.05。