DataFrame中，日期为index，一列数据为收盘价，另一列数据为对数收益，请使用statsmodels对对数收益进行自相关性分析，并用plot_acf进行可视化。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf

# 1. 创建示例数据（日期索引，收盘价和对数收益列）
# np.random.seed(42)
# date_rng = pd.date_range(start='2024-01-01', periods=250, freq='D')
# prices = 100 + np.cumsum(np.random.normal(0.1, 0.5, 250))  # 模拟股价
# log_returns = np.log(prices[1:]/prices[:-1])  # 计算对数收益率

# # 创建DataFrame
# df = pd.DataFrame({
#     'Close': prices[1:],
#     'Log_Return': log_returns
# }, index=date_rng[1:])

# 2. 自相关性分析及可视化
plt.figure(figsize=(12, 6))

# 绘制对数收益率的自相关函数(ACF)图
plot_acf(df['对数收益'].dropna(),  # 确保无缺失值
         lags=40,                    # 显示40个滞后阶数
         alpha=0.05,                 # 95%置信区间
         title='对数收益率自相关函数(ACF)图',
         zero=False,                 # 不显示0阶自相关
         auto_ylims=True,            # 自动调整Y轴范围
         color='darkblue')           # 设置颜色

plt.xlabel('滞后阶数', fontsize=12)
plt.ylabel('自相关系数', fontsize=12)
plt.grid(alpha=0.3)
plt.tight_layout()
plt.show()

# 3. 定量分析：计算不同滞后阶数的自相关系数
from statsmodels.tsa.stattools import acf

# 计算前10个滞后阶数的自相关系数
acf_values = acf(df['对数收益'].dropna(), nlags=10, fft=False, alpha=0.05)

# 输出自相关系数及置信区间
print("\n对数收益率自相关系数分析:")
print(f"{'滞后阶数':<8}{'自相关系数':<15}{'95%置信区间':<25}")
for i, (coef, conf_int) in enumerate(zip(acf_values[0], acf_values[1])):
    if i == 0:  # 跳过0阶自相关（总是1）
        continue
    print(f"Lag {i:<6}{coef:.4f}{'':<10}({conf_int[0]:.4f}, {conf_int[1]:.4f})")

# Python代码
# 我们可以使用statsmodels来进行分析
import statsmodels.api as sm

# 计算对数收益的自相关性
log_returns = df['对数收益']

# 创建ACF图
sm.graphics.tsa.plot_acf(log_returns, lags=40, alpha=0.05)  # 这里的lags表示滞后期数，可根据需要进行调整
plt.title('对数收益的自相关性')
plt.savefig('图4-7.jpg', dpi=300)
plt.show()

下面用plot_acf分别分析DataFrame中对数收益平方及绝对值的自相关性，要求结果是2行子图，第一行是对数收益平方的自相关性，第二行是对数收益绝对值的自相关性。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.graphics.tsaplots import plot_acf

# 1. 准备示例数据（日期索引，收盘价和对数收益列）
# np.random.seed(42)
# date_rng = pd.date_range(start='2024-01-01', periods=250, freq='D')
# prices = 100 + np.cumsum(np.random.normal(0.1, 0.5, 250))  # 模拟股价
# log_returns = np.log(prices[1:]/prices[:-1])  # 计算对数收益率

# df = pd.DataFrame({
#     'Close': prices[1:],
#     '对数收益': log_returns
# }, index=date_rng[1:])

# 2. 创建2行1列的子图
fig, axes = plt.subplots(nrows=2, ncols=1, figsize=(12, 10), dpi=100)
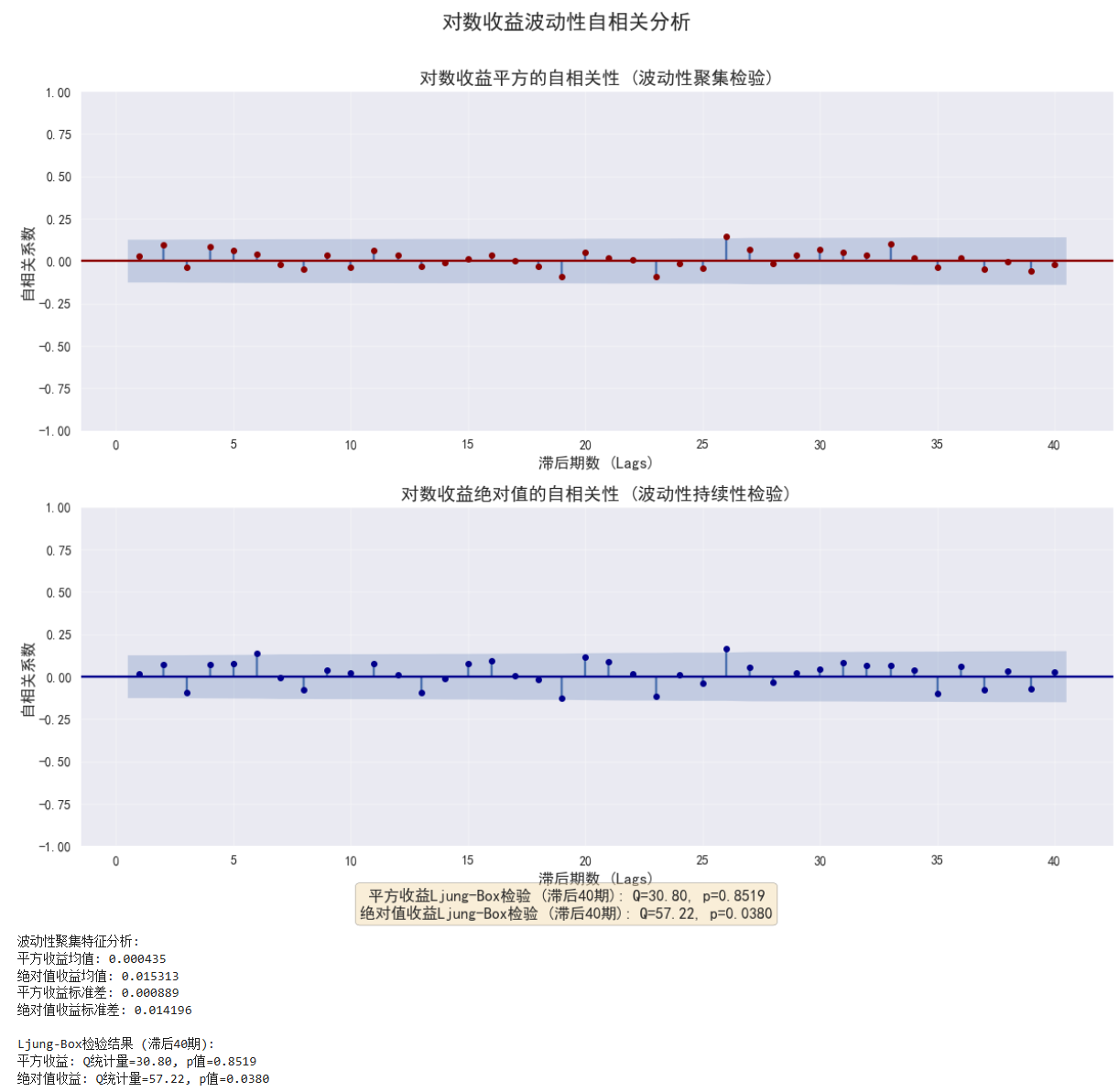
fig.suptitle('对数收益波动性自相关分析', fontsize=16, fontweight='bold')

# 3. 第一子图：对数收益平方的自相关图
squared_returns = df['对数收益'] ** 2  # 计算对数收益的平方
plot_acf(squared_returns, lags=40, alpha=0.05, ax=axes[0], 
         title='', color='darkred', zero=False)
axes[0].set_title('对数收益平方的自相关性 (波动性聚集检验)', fontsize=14)
axes[0].set_xlabel('滞后期数 (Lags)', fontsize=12)
axes[0].set_ylabel('自相关系数', fontsize=12)
axes[0].grid(alpha=0.3)

# 4. 第二子图：对数收益绝对值的自相关图
abs_returns = np.abs(df['对数收益'])  # 计算对数收益的绝对值
plot_acf(abs_returns, lags=40, alpha=0.05, ax=axes[1], 
         title='', color='darkblue', zero=False)
axes[1].set_title('对数收益绝对值的自相关性 (波动性持续性检验)', fontsize=14)
axes[1].set_xlabel('滞后期数 (Lags)', fontsize=12)
axes[1].set_ylabel('自相关系数', fontsize=12)
axes[1].grid(alpha=0.3)

# 5. 添加统计检验结果
lb_test_squared = sm.stats.acorr_ljungbox(squared_returns, lags=40, return_df=True)
lb_test_abs = sm.stats.acorr_ljungbox(abs_returns, lags=40, return_df=True)

stats_text = (
    f"平方收益Ljung-Box检验 (滞后40期): Q={lb_test_squared['lb_stat'].iloc[-1]:.2f}, p={lb_test_squared['lb_pvalue'].iloc[-1]:.4f}\n"
    f"绝对值收益Ljung-Box检验 (滞后40期): Q={lb_test_abs['lb_stat'].iloc[-1]:.2f}, p={lb_test_abs['lb_pvalue'].iloc[-1]:.4f}"
)

fig.text(0.5, 0.01, stats_text, fontsize=12, ha='center', 
         bbox=dict(boxstyle='round', facecolor='wheat', alpha=0.5))

# 6. 调整布局并保存
plt.tight_layout(rect=[0, 0.03, 1, 0.97])  # 为总标题和统计文本留空间
plt.savefig('volatility_autocorrelation_analysis.jpg', dpi=300, bbox_inches='tight')
plt.show()

# 7. 输出关键统计指标
print("波动性聚集特征分析:")
print(f"平方收益均值: {squared_returns.mean():.6f}")
print(f"绝对值收益均值: {abs_returns.mean():.6f}")
print(f"平方收益标准差: {squared_returns.std():.6f}")
print(f"绝对值收益标准差: {abs_returns.std():.6f}")
print("\nLjung-Box检验结果 (滞后40期):")
print(f"平方收益: Q统计量={lb_test_squared['lb_stat'].iloc[-1]:.2f}, p值={lb_test_squared['lb_pvalue'].iloc[-1]:.4f}")
print(f"绝对值收益: Q统计量={lb_test_abs['lb_stat'].iloc[-1]:.2f}, p值={lb_test_abs['lb_pvalue'].iloc[-1]:.4f}")