现在我已经准备好了股票收益数据以及市场收益率数据，它们被分别存储在名为df的DataFrame和Hs300的DataFrame中，这两个DataFrame都是以日期为index，包含的数据都是每日的收盘价，现在我需要使用Python创建CAPM模型，计算出该股票的贝塔系数，请给出示例代码。

import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt

# 1. 数据预处理
# 合并股票和沪深300数据
merged_df = pd.concat([df['收盘'], hs300['close']], axis=1)
merged_df.columns = ['stock', 'market']

# 计算日收益率（使用对数收益率更符合金融特性）
returns = merged_df.pct_change().dropna()
# returns = np.log(merged_df / merged_df.shift(1)).dropna()  # 对数收益率

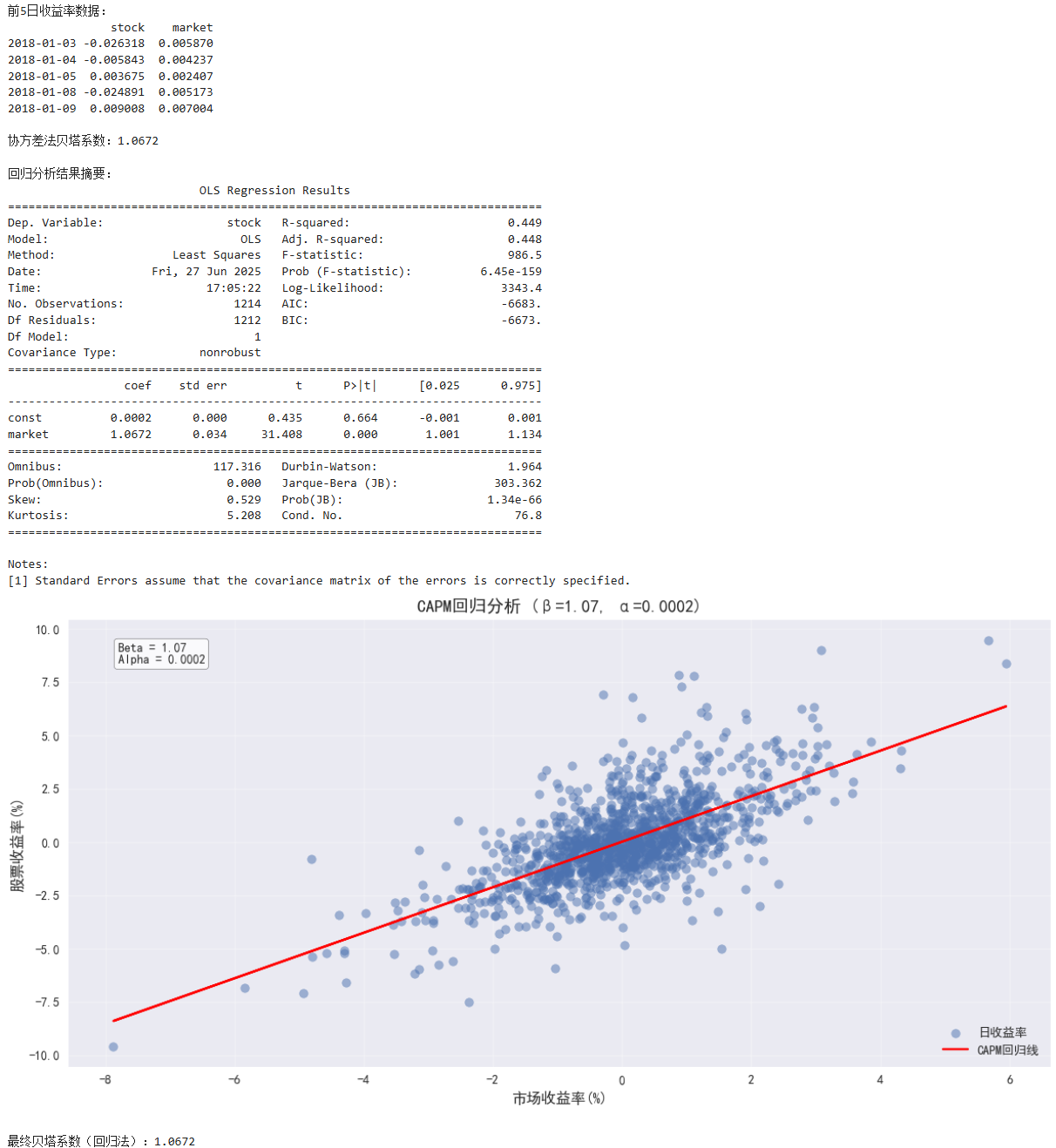
print("前5日收益率数据：")
print(returns.head())

# 2. 协方差法计算贝塔
cov_matrix = returns.cov()
cov_stock_market = cov_matrix.loc['stock', 'market']  # 股票与市场的协方差
market_variance = returns['market'].var()             # 市场方差
beta_cov = cov_stock_market / market_variance

print(f"\n协方差法贝塔系数：{beta_cov:.4f}")

# 3. 回归法计算贝塔（CAPM标准方法）
# 准备回归数据
X = returns['market']          # 自变量：市场收益率
y = returns['stock']           # 因变量：股票收益率
X = sm.add_constant(X)         # 添加截距项

# 拟合线性回归模型
model = sm.OLS(y, X).fit()
beta_regression = model.params['market']
alpha = model.params['const']

# 输出回归结果
print("\n回归分析结果摘要：")
print(model.summary())

# 4. 可视化分析
plt.figure(figsize=(12, 6))

# 绘制收益率散点图与回归线
plt.scatter(returns['market']*100, returns['stock']*100, alpha=0.5, label='日收益率')
plt.plot(returns['market']*100, (alpha + beta_regression*returns['market'])*100, 
         color='red', label='CAPM回归线')
plt.xlabel('市场收益率(%)', fontsize=12)
plt.ylabel('股票收益率(%)', fontsize=12)
plt.title(f'CAPM回归分析 (β={beta_regression:.2f}, α={alpha:.4f})', fontsize=14)
plt.legend()
plt.grid(alpha=0.3)

# 添加Beta值标注
plt.text(0.05, 0.95, 
         f'Beta = {beta_regression:.2f}\nAlpha = {alpha:.4f}',
         transform=plt.gca().transAxes,
         verticalalignment='top',
         bbox=dict(boxstyle='round', facecolor='white', alpha=0.8))

plt.tight_layout()
plt.show()

# 5. 输出最终贝塔系数
print(f"\n最终贝塔系数（回归法）：{beta_regression:.4f}")