提示词

现在有一个DataFrame，名为asset_df，其中包含一个投资组合AAPL、AMZN、GOOG、MSFT的月度收益，持仓比例都是25%。另外一个DataFrame，名为factors，其中包含了月度三因子数据。DataFrame中包含的列有MKT-RF、SMB、HML和RF。需要使用这两个DataFrame演示三因子模型的滚动估计，并将结果进行可视化，请给出示例代码。

答案

import pandas as pd
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
from matplotlib.ticker import PercentFormatter

# 1. 数据准备
# 假设asset_df包含四只股票的月度收益率，列为['AAPL', 'AMZN', 'GOOG', 'MSFT']
# 假设factors包含三因子数据，列为['MKT-RF', 'SMB', 'HML', 'RF']

# 计算等权重投资组合的月度收益率
portfolio_return = asset_df.mean(axis=1)  # 25%等权重组合
portfolio_return.name = 'Portfolio'

# 合并因子数据
full_data = pd.concat([portfolio_return, factors], axis=1).dropna()

# 计算投资组合超额收益
full_data['Portfolio_Excess'] = full_data['Portfolio'] - full_data['RF']

# 2. 滚动三因子模型
WINDOW_SIZE = 36  # 3年滚动窗口
dates = []
alphas = []
betas_mkt = []
betas_smb = []
betas_hml = []
r_squared = []

print("开始滚动三因子模型估计...")
for i in range(WINDOW_SIZE, len(full_data)):
    # 获取当前窗口数据
    window_data = full_data.iloc[i-WINDOW_SIZE:i]
  
    # 准备回归数据
    X = window_data[['Mkt-RF', 'SMB', 'HML']]
    X = sm.add_constant(X)  # 添加截距项
    y = window_data['Portfolio_Excess']
  
    # 拟合三因子模型
    model = sm.OLS(y, X).fit()
  
    # 存储结果
    dates.append(full_data.index[i])
    alphas.append(model.params['const'])
    betas_mkt.append(model.params['Mkt-RF'])
    betas_smb.append(model.params['SMB'])
    betas_hml.append(model.params['HML'])
    r_squared.append(model.rsquared)

# 创建结果DataFrame
results = pd.DataFrame({
    'Date': dates,
    'Alpha': alphas,
    'Beta_Mkt': betas_mkt,
    'Beta_SMB': betas_smb,
    'Beta_HML': betas_hml,
    'R_squared': r_squared
}).set_index('Date')

# 3. 可视化结果
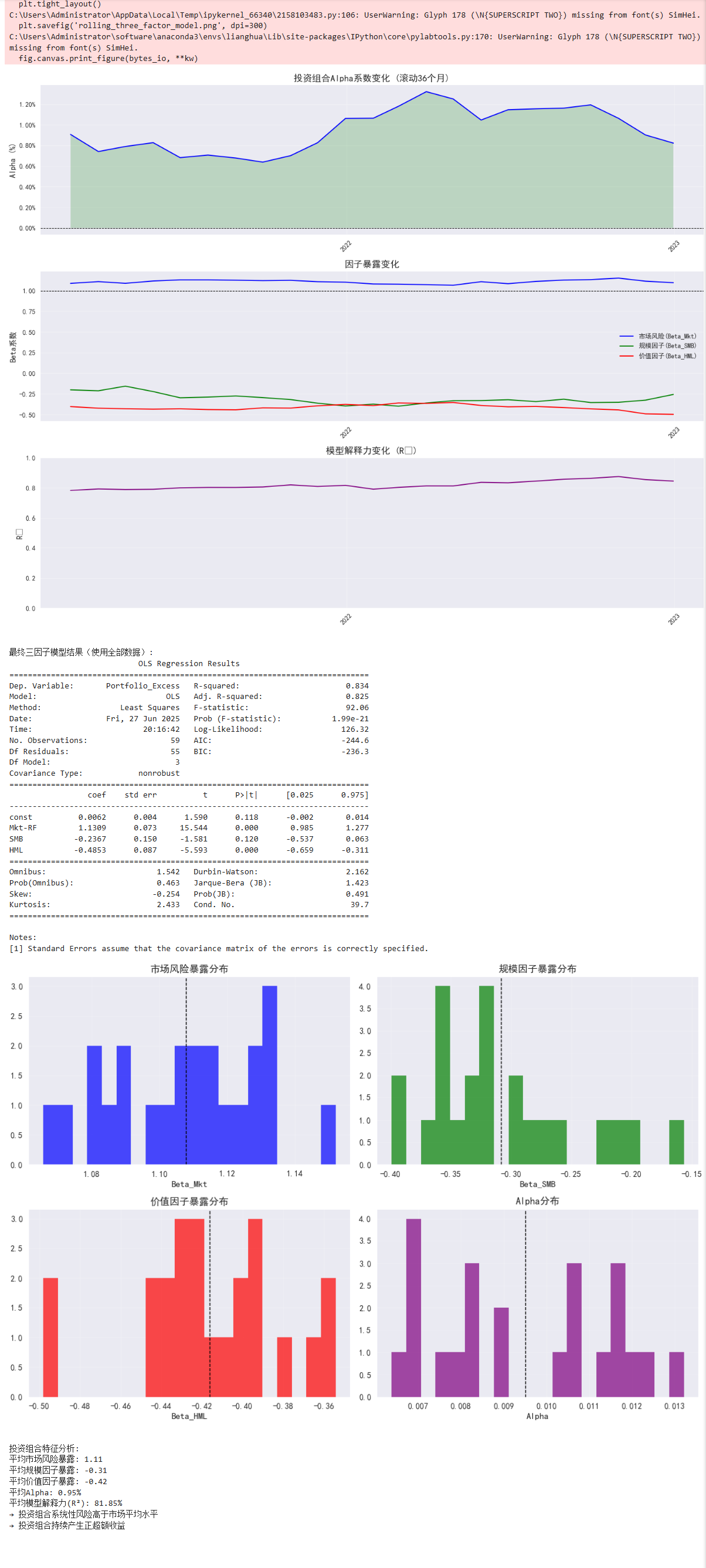
plt.figure(figsize=(15, 12))

# 3.1 Alpha系数变化
plt.subplot(3, 1, 1)
plt.plot(results.index, results['Alpha'], 'b-', lw=1.5)
plt.fill_between(results.index, results['Alpha'], 0, 
                 where=(results['Alpha'] > 0), 
                 facecolor='green', alpha=0.2)
plt.fill_between(results.index, results['Alpha'], 0, 
                 where=(results['Alpha'] < 0), 
                 facecolor='red', alpha=0.2)
plt.axhline(0, color='black', linestyle='--', lw=0.8)
plt.title('投资组合Alpha系数变化 (滚动36个月)', fontsize=14)
plt.ylabel('Alpha (%)', fontsize=12)
plt.gca().yaxis.set_major_formatter(PercentFormatter(1.0))  # 转换为百分比格式
plt.grid(alpha=0.3)

# 3.2 Beta系数变化
plt.subplot(3, 1, 2)
plt.plot(results.index, results['Beta_Mkt'], 'b-', label='市场风险(Beta_Mkt)', lw=1.5)
plt.plot(results.index, results['Beta_SMB'], 'g-', label='规模因子(Beta_SMB)', lw=1.5)
plt.plot(results.index, results['Beta_HML'], 'r-', label='价值因子(Beta_HML)', lw=1.5)
plt.axhline(1, color='black', linestyle='--', lw=0.8)
plt.title('因子暴露变化', fontsize=14)
plt.ylabel('Beta系数', fontsize=12)
plt.legend(loc='best')
plt.grid(alpha=0.3)

# 3.3 R²变化
plt.subplot(3, 1, 3)
plt.plot(results.index, results['R_squared'], 'purple', lw=1.5)
plt.title('模型解释力变化 (R²)', fontsize=14)
plt.ylabel('R²', fontsize=12)
plt.ylim(0, 1)
plt.grid(alpha=0.3)

# 设置x轴日期格式
for ax in plt.gcf().axes:
    ax.xaxis.set_major_locator(mdates.YearLocator())
    ax.xaxis.set_major_formatter(mdates.DateFormatter('%Y'))
    plt.setp(ax.xaxis.get_majorticklabels(), rotation=45)

plt.tight_layout()
plt.savefig('rolling_three_factor_model.png', dpi=300)
plt.show()

# 4. 最终模型结果（使用全部数据）
X_full = full_data[['Mkt-RF', 'SMB', 'HML']]
X_full = sm.add_constant(X_full)
y_full = full_data['Portfolio_Excess']

final_model = sm.OLS(y_full, X_full).fit()
print("\n最终三因子模型结果（使用全部数据）:")
print(final_model.summary())

# 5. 因子暴露分布分析
plt.figure(figsize=(12, 8))

# 5.1 Beta分布直方图
plt.subplot(2, 2, 1)
plt.hist(results['Beta_Mkt'], bins=20, color='blue', alpha=0.7)
plt.axvline(results['Beta_Mkt'].mean(), color='k', linestyle='dashed', linewidth=1)
plt.title('市场风险暴露分布')
plt.xlabel('Beta_Mkt')
plt.grid(alpha=0.2)

plt.subplot(2, 2, 2)
plt.hist(results['Beta_SMB'], bins=20, color='green', alpha=0.7)
plt.axvline(results['Beta_SMB'].mean(), color='k', linestyle='dashed', linewidth=1)
plt.title('规模因子暴露分布')
plt.xlabel('Beta_SMB')
plt.grid(alpha=0.2)

plt.subplot(2, 2, 3)
plt.hist(results['Beta_HML'], bins=20, color='red', alpha=0.7)
plt.axvline(results['Beta_HML'].mean(), color='k', linestyle='dashed', linewidth=1)
plt.title('价值因子暴露分布')
plt.xlabel('Beta_HML')
plt.grid(alpha=0.2)

plt.subplot(2, 2, 4)
plt.hist(results['Alpha'], bins=20, color='purple', alpha=0.7)
plt.axvline(results['Alpha'].mean(), color='k', linestyle='dashed', linewidth=1)
plt.title('Alpha分布')
plt.xlabel('Alpha')
plt.grid(alpha=0.2)

plt.tight_layout()
plt.show()

# 6. 结果解读
print("\n投资组合特征分析:")
print(f"平均市场风险暴露: {results['Beta_Mkt'].mean():.2f}")
print(f"平均规模因子暴露: {results['Beta_SMB'].mean():.2f}")
print(f"平均价值因子暴露: {results['Beta_HML'].mean():.2f}")
print(f"平均Alpha: {results['Alpha'].mean():.2%}")
print(f"平均模型解释力(R²): {results['R_squared'].mean():.2%}")

if results['Beta_Mkt'].mean() > 1:
    print("→ 投资组合系统性风险高于市场平均水平")
else:
    print("→ 投资组合系统性风险低于市场平均水平")

if results['Alpha'].mean() > 0:
    print("→ 投资组合持续产生正超额收益")
else:
    print("→ 投资组合未能产生正超额收益")

结果：

AI用三因子模型对投资组合进行滚动估计

提示词

答案