1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
| import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from arch import arch_model
# 1. 数据准备
# 假设df是包含日期索引和'收盘价'列的DataFrame
# 计算日收益率(百分比形式)
# df['收益率'] = df['收盘价'].pct_change().dropna() * 100
# returns = df['收益率'].dropna()
# 2. 拟合GARCH(1,1)模型
# 使用均值方程(Constant)和GARCH波动率模型
model = arch_model(
returns,
mean='Constant', # 常数均值模型
vol='Garch', # GARCH波动率模型
p=1, q=1, # GARCH(1,1)模型
dist='t' # 使用t分布考虑厚尾特征
)
# 拟合模型
result = model.fit(disp='off', show_warning=False)
# 3. 输出模型结果
print("\n" + "="*80)
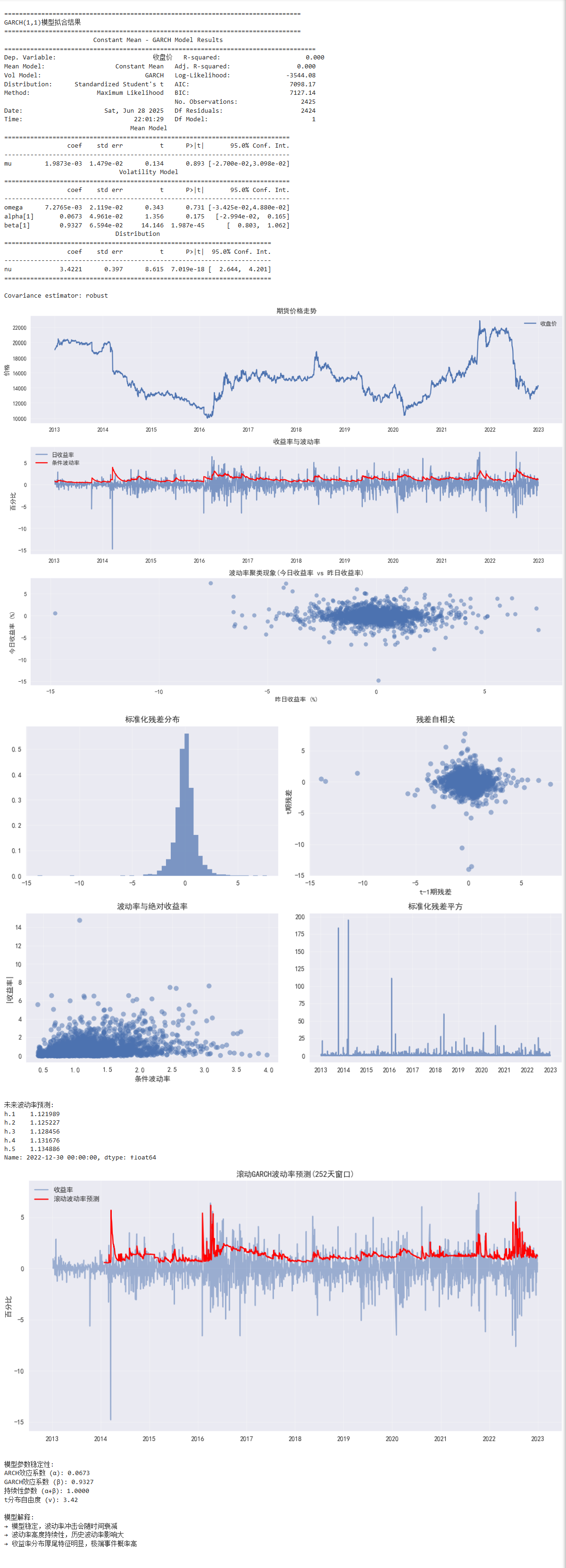
print("GARCH(1,1)模型拟合结果")
print("="*80)
print(result.summary())
# 提取关键参数
omega = result.params['omega']
alpha = result.params['alpha[1]']
beta = result.params['beta[1]']
nu = result.params['nu'] # t分布自由度
# 4. 添加条件波动率到DataFrame
df['条件波动率'] = result.conditional_volatility
# 5. 可视化结果
plt.figure(figsize=(14, 10))
# 5.1 原始价格序列
plt.subplot(3, 1, 1)
plt.plot(df['收盘价'], label='收盘价')
plt.title('期货价格走势')
plt.ylabel('价格')
plt.grid(alpha=0.3)
plt.legend()
# 5.2 收益率与条件波动率
plt.subplot(3, 1, 2)
plt.plot(returns, label='日收益率', alpha=0.7)
plt.plot(df['条件波动率'], label='条件波动率', color='red')
plt.title('收益率与波动率')
plt.ylabel('百分比')
plt.grid(alpha=0.3)
plt.legend()
# 5.3 波动率聚类现象
plt.subplot(3, 1, 3)
plt.scatter(returns, returns.shift(1), alpha=0.5)
plt.title('波动率聚类现象(今日收益率 vs 昨日收益率)')
plt.xlabel('昨日收益率 (%)')
plt.ylabel('今日收益率 (%)')
plt.grid(alpha=0.3)
plt.tight_layout()
plt.savefig('garch_results.png', dpi=300)
plt.show()
# 6. 模型诊断
# 6.1 标准化残差分析
std_resid = result.resid / result.conditional_volatility
plt.figure(figsize=(12, 8))
plt.subplot(2, 2, 1)
plt.hist(std_resid, bins=50, density=True, alpha=0.7)
plt.title('标准化残差分布')
plt.grid(alpha=0.3)
plt.subplot(2, 2, 2)
plt.scatter(std_resid, std_resid.shift(1), alpha=0.5)
plt.title('残差自相关')
plt.xlabel('t-1期残差')
plt.ylabel('t期残差')
plt.grid(alpha=0.3)
plt.subplot(2, 2, 3)
plt.scatter(result.conditional_volatility, np.abs(returns), alpha=0.5)
plt.title('波动率与绝对收益率')
plt.xlabel('条件波动率')
plt.ylabel('|收益率|')
plt.grid(alpha=0.3)
plt.subplot(2, 2, 4)
plt.plot(std_resid**2, alpha=0.7)
plt.title('标准化残差平方')
plt.grid(alpha=0.3)
plt.tight_layout()
plt.savefig('garch_diagnostics.png', dpi=300)
plt.show()
# 7. 波动率预测
# 预测未来5天的波动率
forecast = result.forecast(horizon=5)
future_vol = np.sqrt(forecast.variance.iloc[-1])
print("\n未来波动率预测:")
print(future_vol)
# 8. 高级分析 - 滚动波动率预测
rolling_vol = pd.Series(index=returns.index, dtype=float)
window_size = 252 # 1年交易日的滚动窗口
for i in range(window_size, len(returns)):
train_data = returns.iloc[i-window_size:i]
model = arch_model(train_data, mean='Constant', vol='Garch', p=1, q=1)
res = model.fit(disp='off', show_warning=False)
rolling_vol.iloc[i] = res.conditional_volatility.iloc[-1]
# 可视化滚动预测
plt.figure(figsize=(12, 6))
plt.plot(returns, label='收益率', alpha=0.5)
plt.plot(rolling_vol, label='滚动波动率预测', color='red')
plt.title('滚动GARCH波动率预测(252天窗口)')
plt.ylabel('百分比')
plt.grid(alpha=0.3)
plt.legend()
plt.tight_layout()
plt.savefig('rolling_garch_volatility.png', dpi=300)
plt.show()
# 9. 模型参数稳定性检验
print("\n模型参数稳定性:")
print(f"ARCH效应系数 (α): {alpha:.4f}")
print(f"GARCH效应系数 (β): {beta:.4f}")
print(f"持续性参数 (α+β): {alpha+beta:.4f}")
print(f"t分布自由度 (ν): {nu:.2f}")
# 10. 模型解释
print("\n模型解释:")
if alpha + beta < 1:
print("→ 模型稳定,波动率冲击会随时间衰减")
else:
print("→ 模型可能不稳定,波动率冲击具有持续性")
if alpha > 0.1:
print("→ 市场对短期冲击敏感,波动率响应强烈")
elif alpha < 0.05:
print("→ 市场对短期冲击反应温和")
if beta > 0.85:
print("→ 波动率高度持续性,历史波动率影响大")
if nu < 5:
print("→ 收益率分布厚尾特征明显,极端事件概率高")
|