现在有一个名叫returns的Pandas Series，存储的是某股票的每日简单收益，使用Python定义一个函数，用于模拟该数据的几何布朗运动，请给出示例代码。

import numpy as np
import pandas as pd

def simulate_gbm(returns, S0, T=1.0, dt=1/252, num_sims=1000):
    """
    使用几何布朗运动模拟股票价格路径
  
    参数:
    returns : pandas.Series - 股票每日简单收益率
    S0      : float - 初始股票价格
    T       : float - 模拟总时间（年）
    dt      : float - 时间步长（年，默认1/252表示交易日）
    num_sims: int   - 模拟路径数量
  
    返回:
    numpy.ndarray - 形状为(num_steps, num_sims)的模拟价格路径
    """
    # 1. 计算对数收益率
    log_returns = np.log(1 + returns)
  
    # 2. 估计模型参数（年化）
    mu = log_returns.mean() * 252           # 年化漂移率
    sigma = log_returns.std() * np.sqrt(252) # 年化波动率
    adj_drift = mu - 0.5 * sigma**2         # 调整后的漂移项
  
    # 3. 设置时间参数
    num_steps = int(T / dt)  # 总步数
  
    # 4. 生成随机路径
    dW = np.random.normal(0, np.sqrt(dt), size=(num_steps, num_sims))  # 维纳过程增量
    price_paths = np.zeros((num_steps, num_sims))
    price_paths[0] = S0  # 设置初始价格
  
    # 5. 迭代计算价格路径
    for t in range(1, num_steps):
        price_paths[t] = price_paths[t-1] * np.exp(
            adj_drift * dt + sigma * dW[t]
        )
  
    return price_paths

# 示例用法
if __name__ == "__main__":
    # 生成示例收益率数据（假设有252个交易日）
    # np.random.seed(42)
    # returns = pd.Series(np.random.normal(0.001, 0.02, 252))
  
    # 模拟参数
    S0 = returns.loc[returns.index[-1],]    # 初始价格
    T = 1.0       # 1年
    dt = 1/252    # 每日时间步长
    num_sims = 5  # 模拟5条路径
  
    # 运行模拟
    paths = simulate_gbm(returns, S0, T, dt, num_sims)
  
    # 可视化结果
    import matplotlib.pyplot as plt
  
    plt.figure(figsize=(12, 6))
    for i in range(num_sims):
        plt.plot(paths[:, i])
    plt.title('几何布朗运动 - 股票价格模拟')
    plt.xlabel('交易日')
    plt.ylabel('价格')
    plt.grid(alpha=0.3)
    plt.show()

# Python代码
# 首先我们需要将数据拆分一下
train = returns['2022']
test = returns['2023']

# 然后我们使用训练集计算相关参数
T = len(test)
N = len(test)
S_0 = df.loc[train.index[-1], "收盘"]# 初始的股票价格
N_SIM = 50 # 模拟的次数
mu = train.mean()# 公式中的mu
sigma = train.std()# 公式中的sigma
def geometric_brownian_motion(s_0, mu, sigma, n_sims, T, N, random_seed=42):  
    """  
    定义一个函数，用于模拟股票价格的几何布朗运动过程。  
    参数：  
    s_0: 股票的初始价格  
    mu: 预期年化收益率  
    sigma: 年化波动率  
    n_sims: 模拟次数  
    T: 模拟的总时间（以年为单位）  
    N: 时间步长数，即总时间被分割成的块数  
    random_seed: 随机种子，用于产生随机数（默认为42）  
    返回值：  
    模拟的股票价格序列，形状为(n_sims, N+1)，其中N+1是因为在模拟开始时插入了一个初始价格s_0。  
    """  
    # 设置随机种子，确保每次运行产生的随机数相同
    np.random.seed(random_seed)  
    # 计算时间步长，即每个时间块的大小
    dt = T/N
    # 生成N个标准正态分布的随机扰动项，每个扰动项的大小由时间步长决定
    dW = np.random.normal(scale=np.sqrt(dt),  
                          size=(n_sims, N))   
    # 对每行（每个模拟）的扰动项进行累加，得到W序列 
    W = np.cumsum(dW, axis=1)
    # 创建一个从dt到T的时间步长序列，用于描述整个模拟时间区间
    time_step = np.linspace(dt, T, N)
    # 将时间步长序列扩展到(n_sims, N)的形状，以便于每个模拟都有对应的时间步长
    time_steps = np.broadcast_to(time_step, (n_sims, N))
    # 定义一个表达式，描述股票价格的随机变化过程 
    S_t = ( 
        s_0 * np.exp((mu - 0.5 * sigma**2) * time_steps + sigma * W)  
    )  
    # 在S_t的每行的开头插入初始价格s_0，形成完整的股票价格序列 
    S_t = np.insert(S_t, 0, s_0, axis=1)  
    # 返回模拟的股票价格序列
    return S_t

接下来使用上面定义好的几何布朗运动函数模拟returns数据，并将结果可视化，请给出示例代码。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
from matplotlib.ticker import FuncFormatter

# 运行模拟
simulated_paths = geometric_brownian_motion(S_0, mu, sigma, N_SIM, T, N)

# 创建与测试集对应的时间索引
date_index = pd.date_range(start=train.index[-1], periods=N+1, freq='D')[:N+1]

# ======================
# 可视化部分
# ======================

# 1. 模拟路径与真实价格对比
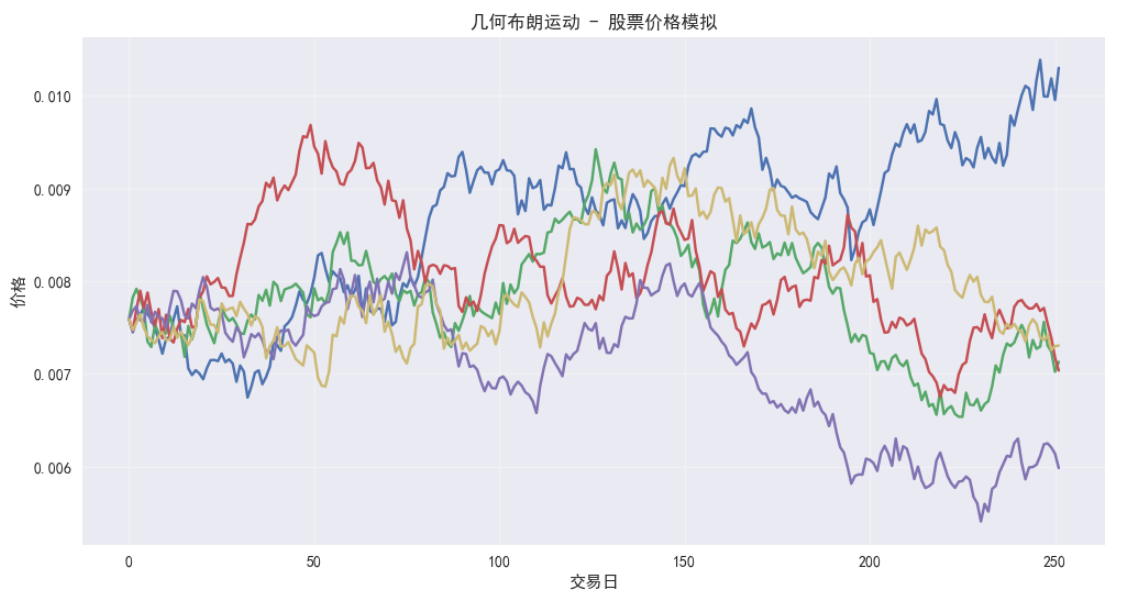
plt.figure(figsize=(14, 7))
plt.title(f"股票价格蒙特卡洛模拟 (N={N_SIM}次)\nμ={mu:.4f}, σ={sigma:.4f}", fontsize=14)

# 绘制所有模拟路径（半透明处理）
for i in range(N_SIM):
    plt.plot(date_index, simulated_paths[i], lw=1, alpha=0.15, color='steelblue')

# 计算并绘制关键统计量
mean_path = np.mean(simulated_paths, axis=0)
upper_95 = np.percentile(simulated_paths, 95, axis=0)
lower_5 = np.percentile(simulated_paths, 5, axis=0)

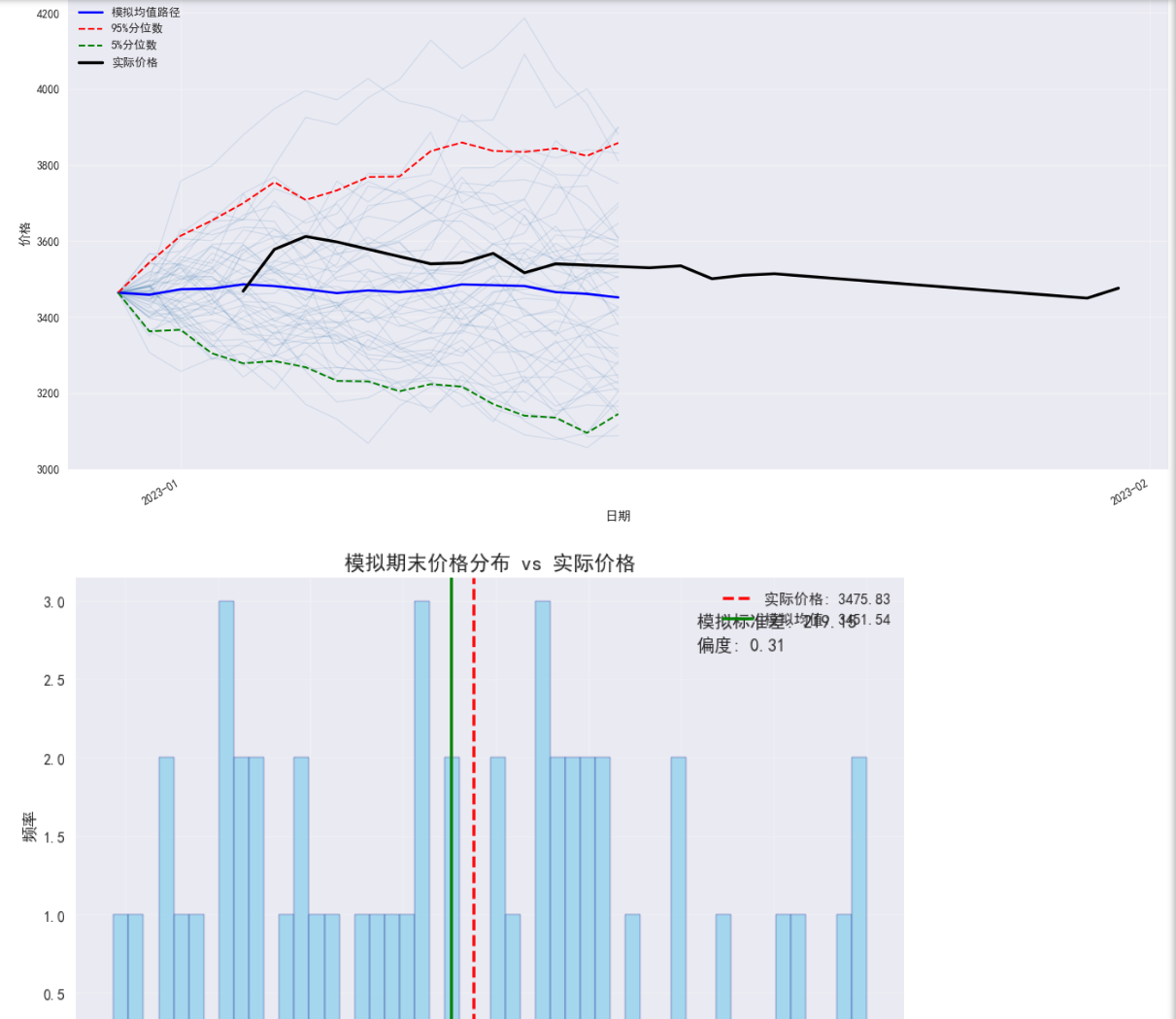
plt.plot(date_index, mean_path, 'b-', lw=2, label='模拟均值路径')
plt.plot(date_index, upper_95, 'r--', lw=1.5, label='95%分位数')
plt.plot(date_index, lower_5, 'g--', lw=1.5, label='5%分位数')

# 添加实际价格曲线（测试期）
test_period = df.loc[test.index, '收盘']
plt.plot(test_period.index, test_period.values, 'k-', lw=2.5, label='实际价格')

# 美化坐标轴
plt.gca().xaxis.set_major_locator(mdates.MonthLocator())
plt.gca().xaxis.set_major_formatter(mdates.DateFormatter('%Y-%m'))
plt.gcf().autofmt_xdate()  # 自动旋转日期标签

# 添加图例和网格
plt.legend(loc='upper left')
plt.grid(True, alpha=0.3)
plt.xlabel('日期')
plt.ylabel('价格')
plt.tight_layout()
plt.savefig('GBM_模拟路径对比.png', dpi=300)
plt.show()

# 2. 模拟路径与真实价格差异分析（最后一天）
final_prices = simulated_paths[:, -1]
actual_final_price = test_period.iloc[-1]

plt.figure(figsize=(10, 6))
plt.hist(final_prices, bins=50, alpha=0.7, color='skyblue', edgecolor='navy')
plt.axvline(x=actual_final_price, color='red', linestyle='--', lw=2, 
            label=f'实际价格: {actual_final_price:.2f}')
plt.axvline(x=np.mean(final_prices), color='green', linestyle='-', lw=2, 
            label=f'模拟均值: {np.mean(final_prices):.2f}')

# 添加统计指标
plt.text(0.75, 0.9, f'模拟标准差: {np.std(final_prices):.2f}',
         transform=plt.gca().transAxes, fontsize=12)
plt.text(0.75, 0.85, f'偏度: {pd.Series(final_prices).skew():.2f}',
         transform=plt.gca().transAxes, fontsize=12)

plt.title('模拟期末价格分布 vs 实际价格', fontsize=14)
plt.xlabel('期末价格')
plt.ylabel('频率')
plt.legend()
plt.grid(alpha=0.2)
plt.savefig('GBM_期末价格分布.png', dpi=300)
plt.show()

# 3. 动态预测区间（随时间变化的置信区间）
plt.figure(figsize=(14, 7))
plt.fill_between(date_index, 
                 np.percentile(simulated_paths, 5, axis=0),
                 np.percentile(simulated_paths, 95, axis=0),
                 color='lightblue', alpha=0.5, label='90%置信区间')

plt.plot(date_index, mean_path, 'b-', lw=2, label='模拟均值')
plt.plot(test_period.index, test_period.values, 'k-', lw=2.5, label='实际价格')

# 标记关键事件点
max_dev_idx = np.argmax(np.abs(test_period.values - mean_path[1:]))
event_date = test_period.index[max_dev_idx]
plt.axvline(x=event_date, color='purple', linestyle=':', alpha=0.8)
plt.text(event_date, plt.ylim()[0]*0.95, f'最大偏离点\n{event_date.strftime("%Y-%m-%d")}', 
         ha='center', fontsize=9)

plt.title('GBM模拟的90%置信区间与实际价格对比', fontsize=14)
plt.xlabel('日期')
plt.ylabel('价格')
plt.legend(loc='upper left')
plt.gca().xaxis.set_major_locator(mdates.MonthLocator(interval=2))
plt.gca().xaxis.set_major_formatter(mdates.DateFormatter('%Y-%m'))
plt.gcf().autofmt_xdate()
plt.grid(alpha=0.3)
plt.tight_layout()
plt.savefig('GBM_动态置信区间.png', dpi=300)
plt.show()

# 4. 计算预测误差指标
simulated_mean = mean_path[1:]
actual_prices = test_period.values

mae = np.mean(np.abs(simulated_mean - actual_prices))
rmse = np.sqrt(np.mean((simulated_mean - actual_prices)**2))

print("\n模型性能评估:")
print(f"平均绝对误差(MAE): {mae:.4f}")
print(f"均方根误差(RMSE): {rmse:.4f}")
print(f"年化波动率预测: {sigma:.4f} (实际: {test.std()*np.sqrt(252):.4f})")

# 5. 关键日期对比表
compare_dates = [test_period.index[0], test_period.index[len(test)//2], test_period.index[-1]]
compare_data = []

valid_dates = [d for d in compare_dates if d in date_index]
# valid_dates

for date in valid_dates:
    idx = np.where(date_index == date)[0][0]
    actual = df.loc[date, '收盘']
    sim_mean = mean_path[idx]
    sim_median = np.median(simulated_paths[:, idx])
  
    compare_data.append([
        date.strftime('%Y-%m-%d'),
        actual,
        sim_mean,
        sim_median,
        actual - sim_mean
    ])

# 创建对比表格
compare_df = pd.DataFrame(compare_data, 
                          columns=['日期', '实际价格', '模拟均值', '模拟中位数', '偏差'])
print("\n关键日期价格对比:")
print(compare_df.to_string(index=False))