1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
| import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.stats import genpareto
# 假设returns是包含两列股票收益的DataFrame(列名:stock1, stock2)
# 生成示例数据(实际使用时替换为您的returns)
# np.random.seed(42)
# dates = pd.date_range(start="2024-01-01", periods=500)
# returns = pd.DataFrame({
# 'stock1': np.random.normal(0.001, 0.02, 500),
# 'stock2': np.random.normal(0.0005, 0.015, 500)
# }, index=dates)
# ===== 1. 计算投资组合收益(等权重)=====
weights = np.array([0.5, 0.5]) # 等权重
portfolio_returns = returns.dot(weights) # 组合每日收益
# ===== 2. 计算历史模拟法VaR(95%置信度)=====
confidence_level = 0.95
sorted_returns = np.sort(portfolio_returns) # 收益从小到大排序
var_index = int(len(sorted_returns) * (1 - confidence_level))
var_value = -sorted_returns[var_index] # VaR取正值(损失金额)
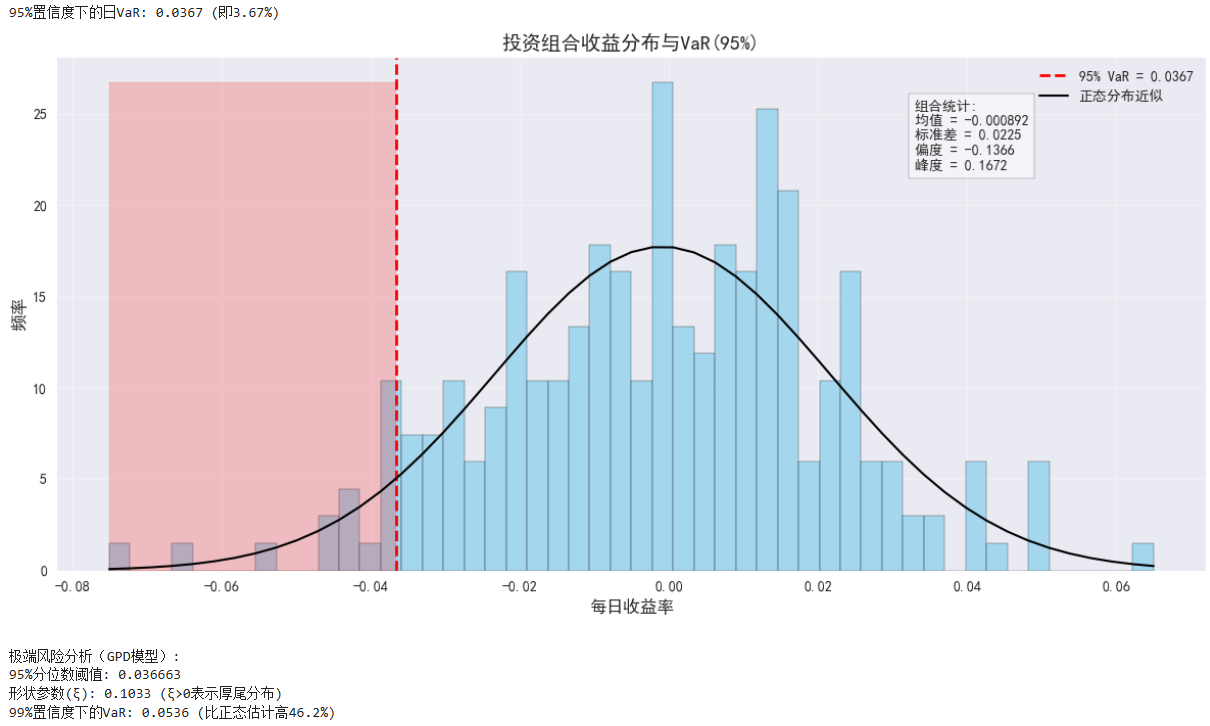
print(f"95%置信度下的日VaR: {var_value:.4f} (即{var_value*100:.2f}%)")
# ===== 3. 直方图可视化VaR结果 =====
plt.figure(figsize=(12, 6))
# 绘制收益分布直方图
n, bins, patches = plt.hist(
portfolio_returns,
bins=50,
alpha=0.7,
color='skyblue',
edgecolor='black',
density=True
)
# 标注VaR线
plt.axvline(x=-var_value, color='red', linestyle='--', linewidth=2,
label=f'95% VaR = {var_value:.4f}')
plt.fill_betweenx([0, max(n)], -var_value, sorted_returns.min(),
color='red', alpha=0.2)
# 添加分布曲线
plt.plot(bins,
norm.pdf(bins, portfolio_returns.mean(), portfolio_returns.std()),
'k-', linewidth=1.5, label='正态分布近似')
# 美化图表
plt.title('投资组合收益分布与VaR(95%)', fontsize=14)
plt.xlabel('每日收益率', fontsize=12)
plt.ylabel('频率', fontsize=12)
plt.legend()
plt.grid(alpha=0.3)
# 添加统计信息框
stats_text = (
f"组合统计:\n"
f"均值 = {portfolio_returns.mean():.6f}\n"
f"标准差 = {portfolio_returns.std():.4f}\n"
f"偏度 = {pd.Series(portfolio_returns).skew():.4f}\n"
f"峰度 = {pd.Series(portfolio_returns).kurtosis():.4f}"
)
plt.gcf().text(0.75, 0.75, stats_text, bbox=dict(facecolor='white', alpha=0.5),
fontsize=10)
plt.tight_layout()
plt.savefig('VaR_visualization.png', dpi=300)
plt.show()
# ===== 4. 极端风险分析(广义帕累托分布)=====
# 计算损失数据(取负收益)
losses = -portfolio_returns
threshold = np.percentile(losses, 95) # 95%分位数作为阈值
exceedances = losses[losses > threshold] - threshold # 超阈值损失
# 拟合广义帕累托分布(GPD)
shape, loc, scale = genpareto.fit(exceedances, floc=0)
# 计算99%置信度下的VaR
alpha = 0.99
n_obs = len(losses)
n_exceed = len(exceedances)
var_gpd = threshold + (scale / shape) * (((1 - alpha) * n_obs / n_exceed) ** (-shape) - 1)
print(f"\n极端风险分析(GPD模型):")
print(f"95%分位数阈值: {threshold:.6f}")
print(f"形状参数(ξ): {shape:.4f} (ξ>0表示厚尾分布)")
print(f"99%置信度下的VaR: {var_gpd:.4f} (比正态估计高{100*(var_gpd/var_value-1):.1f}%)")
|