1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
| import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.cluster.hierarchy import dendrogram, linkage
from scipy.spatial.distance import squareform
# ========== 1. 数据预处理 ==========
def preprocess_data(merged_df):
"""
计算对数收益率和相关性矩阵
"""
# 计算日收益率
returns = merged_df.pct_change().dropna()
# 计算相关性矩阵
corr_matrix = returns.corr()
# 将相关性转换为距离矩阵 (范围[0, 1])
distance_matrix = np.sqrt(0.5 * (1 - corr_matrix))
return returns, corr_matrix, distance_matrix
# ========== 2. 层次聚类与可视化 ==========
def hierarchical_clustering(distance_matrix, asset_names):
"""
执行层次聚类并绘制树状图
"""
# 将距离矩阵转换为压缩形式
condensed_dist = squareform(distance_matrix.values, checks=False)
# 使用平均链接法进行层次聚类
Z = linkage(condensed_dist, method='average')
# 绘制树状图
plt.figure(figsize=(12, 8))
dendrogram(Z, labels=asset_names, orientation='top', leaf_rotation=90)
plt.title('资产层次聚类树状图', fontsize=15)
plt.ylabel('距离', fontsize=12)
plt.tight_layout()
plt.savefig('聚类树状图.png', dpi=300)
plt.show()
return Z
# ========== 3. 准对角化处理 ==========
def quasi_diagonalization(Z, asset_names):
"""
根据聚类结果重新排序资产
"""
# 从树状图中提取排序
order = dendrogram(Z, no_plot=True)['leaves']
# 获取重新排序后的资产名称
ordered_assets = [asset_names[i] for i in order]
return ordered_assets, order
# ========== 4. 递归二分权重分配 ==========
def recursive_bisection(cov, sort_order):
"""
递归分配权重 (HRP核心算法)
"""
# 初始化权重
weights = np.ones(cov.shape[0])
def recursive_step(indices):
n = len(indices)
if n == 1:
return
# 将当前组分为两个子组
mid = n // 2
left = indices[:mid]
right = indices[mid:]
# 计算子组的方差
var_left = _get_cluster_variance(cov, left)
var_right = _get_cluster_variance(cov, right)
# 计算权重调整因子
alpha = 1 - var_left / (var_left + var_right)
# 调整子组权重
weights[left] *= alpha
weights[right] *= (1 - alpha)
# 递归处理子组
recursive_step(left)
recursive_step(right)
# 从根节点开始递归
recursive_step(sort_order)
# 归一化权重
return weights / weights.sum()
def _get_cluster_variance(cov, indices):
"""计算资产簇的方差"""
cov_cluster = cov[np.ix_(indices, indices)]
w = 1 / np.diag(cov_cluster) # 反方差加权
w /= w.sum()
return w.T @ cov_cluster @ w
# ========== 5. 结果分析与可视化 ==========
def plot_asset_weights(weights, asset_names):
"""绘制资产权重分布图"""
plt.figure(figsize=(12, 6))
weights_df = pd.DataFrame({'资产': asset_names, '权重': weights})
weights_df = weights_df.sort_values('权重', ascending=False)
# 绘制柱状图
sns.barplot(x='资产', y='权重', data=weights_df, palette='viridis')
plt.title('HRP资产权重分配', fontsize=15)
plt.xticks(rotation=45)
plt.grid(axis='y', linestyle='--', alpha=0.7)
plt.tight_layout()
plt.savefig('资产权重分布.png', dpi=300)
plt.show()
return weights_df
# ========== 主执行流程 ==========
if __name__ == "__main__":
# 假设merged_df是包含10只股票收盘价的DataFrame
# 列名为股票代码,索引为日期 (已转换为DatetimeIndex)
# 步骤1: 数据预处理
returns, corr_matrix, dist_matrix = preprocess_data(merged_df)
asset_names = returns.columns.tolist()
# 步骤2: 层次聚类与可视化
linkage_matrix = hierarchical_clustering(dist_matrix, asset_names)
# 步骤3: 准对角化
ordered_assets, sort_order = quasi_diagonalization(linkage_matrix, asset_names)
# 可视化重新排序的相关矩阵
plt.figure(figsize=(10, 8))
sns.heatmap(corr_matrix.loc[ordered_assets, ordered_assets],
cmap='coolwarm', center=0, annot=False)
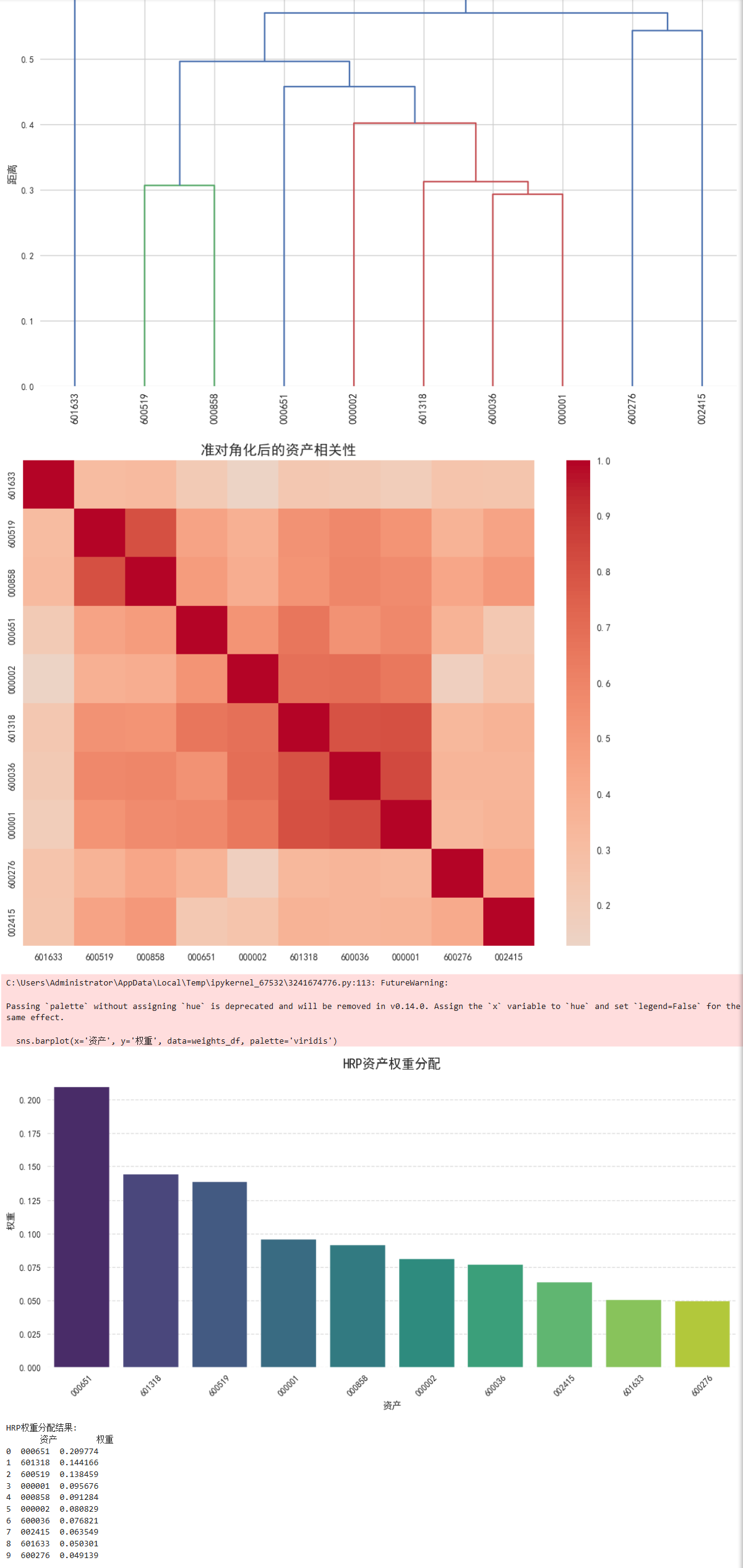
plt.title('准对角化后的资产相关性', fontsize=15)
plt.tight_layout()
plt.savefig('准对角化相关矩阵.png', dpi=300)
plt.show()
# 步骤4: 递归权重分配
cov_matrix = returns.cov() * 252 # 年化协方差矩阵
weights = recursive_bisection(cov_matrix.values, sort_order)
# 步骤5: 结果可视化
weights_df = plot_asset_weights(weights, asset_names)
# 打印权重分配结果
print("HRP权重分配结果:")
print(weights_df.sort_values('权重', ascending=False).reset_index(drop=True))
|