AI用几何布朗运动模拟股价波动
编辑
1
2025-06-29

提示词
现在有一个名叫returns的Pandas Series,存储的是某股票的每日简单收益,使用Python定义一个函数,用于模拟该数据的几何布朗运动,请给出示例代码。
答案
import numpy as np
import pandas as pd
def simulate_gbm(returns, S0, T=1.0, dt=1/252, num_sims=1000):
"""
使用几何布朗运动模拟股票价格路径
参数:
returns : pandas.Series - 股票每日简单收益率
S0 : float - 初始股票价格
T : float - 模拟总时间(年)
dt : float - 时间步长(年,默认1/252表示交易日)
num_sims: int - 模拟路径数量
返回:
numpy.ndarray - 形状为(num_steps, num_sims)的模拟价格路径
"""
# 1. 计算对数收益率
log_returns = np.log(1 + returns)
# 2. 估计模型参数(年化)
mu = log_returns.mean() * 252 # 年化漂移率
sigma = log_returns.std() * np.sqrt(252) # 年化波动率
adj_drift = mu - 0.5 * sigma**2 # 调整后的漂移项
# 3. 设置时间参数
num_steps = int(T / dt) # 总步数
# 4. 生成随机路径
dW = np.random.normal(0, np.sqrt(dt), size=(num_steps, num_sims)) # 维纳过程增量
price_paths = np.zeros((num_steps, num_sims))
price_paths[0] = S0 # 设置初始价格
# 5. 迭代计算价格路径
for t in range(1, num_steps):
price_paths[t] = price_paths[t-1] * np.exp(
adj_drift * dt + sigma * dW[t]
)
return price_paths
# 示例用法
if __name__ == "__main__":
# 生成示例收益率数据(假设有252个交易日)
# np.random.seed(42)
# returns = pd.Series(np.random.normal(0.001, 0.02, 252))
# 模拟参数
S0 = returns.loc[returns.index[-1],] # 初始价格
T = 1.0 # 1年
dt = 1/252 # 每日时间步长
num_sims = 5 # 模拟5条路径
# 运行模拟
paths = simulate_gbm(returns, S0, T, dt, num_sims)
# 可视化结果
import matplotlib.pyplot as plt
plt.figure(figsize=(12, 6))
for i in range(num_sims):
plt.plot(paths[:, i])
plt.title('几何布朗运动 - 股票价格模拟')
plt.xlabel('交易日')
plt.ylabel('价格')
plt.grid(alpha=0.3)
plt.show()
结果:
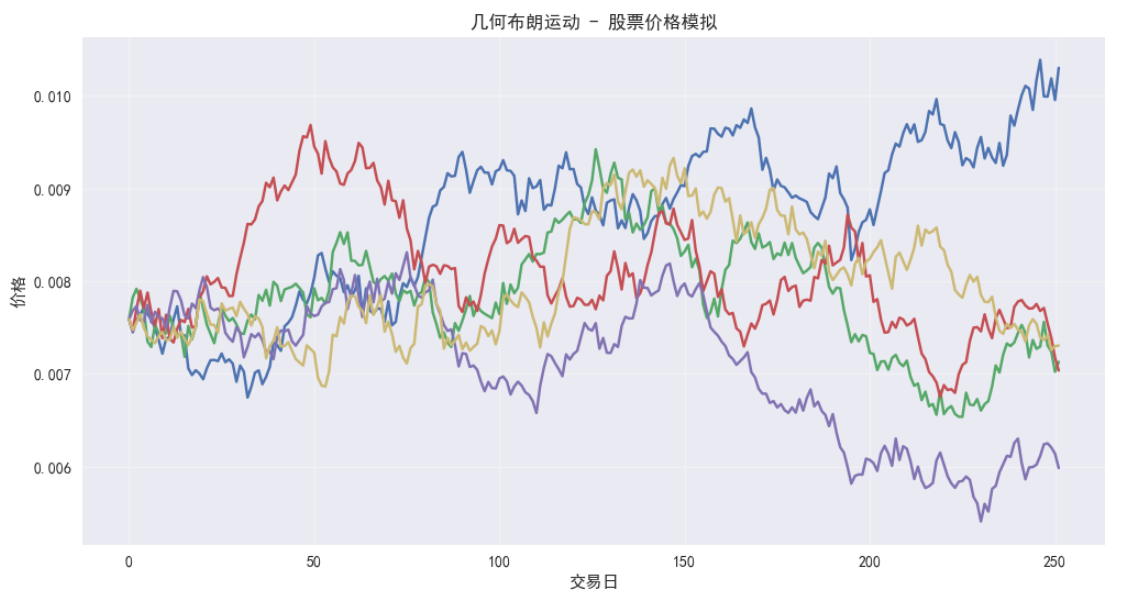
使用定义好的函数模拟股价变动
ai实际一步到位可视化了,不过我们还是简化代码加描述。再来一次
提示词
# Python代码
# 首先我们需要将数据拆分一下
train = returns['2022']
test = returns['2023']
# 然后我们使用训练集计算相关参数
T = len(test)
N = len(test)
S_0 = df.loc[train.index[-1], "收盘"]# 初始的股票价格
N_SIM = 50 # 模拟的次数
mu = train.mean()# 公式中的mu
sigma = train.std()# 公式中的sigma
def geometric_brownian_motion(s_0, mu, sigma, n_sims, T, N, random_seed=42):
"""
定义一个函数,用于模拟股票价格的几何布朗运动过程。
参数:
s_0: 股票的初始价格
mu: 预期年化收益率
sigma: 年化波动率
n_sims: 模拟次数
T: 模拟的总时间(以年为单位)
N: 时间步长数,即总时间被分割成的块数
random_seed: 随机种子,用于产生随机数(默认为42)
返回值:
模拟的股票价格序列,形状为(n_sims, N+1),其中N+1是因为在模拟开始时插入了一个初始价格s_0。
"""
# 设置随机种子,确保每次运行产生的随机数相同
np.random.seed(random_seed)
# 计算时间步长,即每个时间块的大小
dt = T/N
# 生成N个标准正态分布的随机扰动项,每个扰动项的大小由时间步长决定
dW = np.random.normal(scale=np.sqrt(dt),
size=(n_sims, N))
# 对每行(每个模拟)的扰动项进行累加,得到W序列
W = np.cumsum(dW, axis=1)
# 创建一个从dt到T的时间步长序列,用于描述整个模拟时间区间
time_step = np.linspace(dt, T, N)
# 将时间步长序列扩展到(n_sims, N)的形状,以便于每个模拟都有对应的时间步长
time_steps = np.broadcast_to(time_step, (n_sims, N))
# 定义一个表达式,描述股票价格的随机变化过程
S_t = (
s_0 * np.exp((mu - 0.5 * sigma**2) * time_steps + sigma * W)
)
# 在S_t的每行的开头插入初始价格s_0,形成完整的股票价格序列
S_t = np.insert(S_t, 0, s_0, axis=1)
# 返回模拟的股票价格序列
return S_t
接下来使用上面定义好的几何布朗运动函数模拟returns数据,并将结果可视化,请给出示例代码。
答案
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
from matplotlib.ticker import FuncFormatter
# 运行模拟
simulated_paths = geometric_brownian_motion(S_0, mu, sigma, N_SIM, T, N)
# 创建与测试集对应的时间索引
date_index = pd.date_range(start=train.index[-1], periods=N+1, freq='D')[:N+1]
# ======================
# 可视化部分
# ======================
# 1. 模拟路径与真实价格对比
plt.figure(figsize=(14, 7))
plt.title(f"股票价格蒙特卡洛模拟 (N={N_SIM}次)\nμ={mu:.4f}, σ={sigma:.4f}", fontsize=14)
# 绘制所有模拟路径(半透明处理)
for i in range(N_SIM):
plt.plot(date_index, simulated_paths[i], lw=1, alpha=0.15, color='steelblue')
# 计算并绘制关键统计量
mean_path = np.mean(simulated_paths, axis=0)
upper_95 = np.percentile(simulated_paths, 95, axis=0)
lower_5 = np.percentile(simulated_paths, 5, axis=0)
plt.plot(date_index, mean_path, 'b-', lw=2, label='模拟均值路径')
plt.plot(date_index, upper_95, 'r--', lw=1.5, label='95%分位数')
plt.plot(date_index, lower_5, 'g--', lw=1.5, label='5%分位数')
# 添加实际价格曲线(测试期)
test_period = df.loc[test.index, '收盘']
plt.plot(test_period.index, test_period.values, 'k-', lw=2.5, label='实际价格')
# 美化坐标轴
plt.gca().xaxis.set_major_locator(mdates.MonthLocator())
plt.gca().xaxis.set_major_formatter(mdates.DateFormatter('%Y-%m'))
plt.gcf().autofmt_xdate() # 自动旋转日期标签
# 添加图例和网格
plt.legend(loc='upper left')
plt.grid(True, alpha=0.3)
plt.xlabel('日期')
plt.ylabel('价格')
plt.tight_layout()
plt.savefig('GBM_模拟路径对比.png', dpi=300)
plt.show()
# 2. 模拟路径与真实价格差异分析(最后一天)
final_prices = simulated_paths[:, -1]
actual_final_price = test_period.iloc[-1]
plt.figure(figsize=(10, 6))
plt.hist(final_prices, bins=50, alpha=0.7, color='skyblue', edgecolor='navy')
plt.axvline(x=actual_final_price, color='red', linestyle='--', lw=2,
label=f'实际价格: {actual_final_price:.2f}')
plt.axvline(x=np.mean(final_prices), color='green', linestyle='-', lw=2,
label=f'模拟均值: {np.mean(final_prices):.2f}')
# 添加统计指标
plt.text(0.75, 0.9, f'模拟标准差: {np.std(final_prices):.2f}',
transform=plt.gca().transAxes, fontsize=12)
plt.text(0.75, 0.85, f'偏度: {pd.Series(final_prices).skew():.2f}',
transform=plt.gca().transAxes, fontsize=12)
plt.title('模拟期末价格分布 vs 实际价格', fontsize=14)
plt.xlabel('期末价格')
plt.ylabel('频率')
plt.legend()
plt.grid(alpha=0.2)
plt.savefig('GBM_期末价格分布.png', dpi=300)
plt.show()
# 3. 动态预测区间(随时间变化的置信区间)
plt.figure(figsize=(14, 7))
plt.fill_between(date_index,
np.percentile(simulated_paths, 5, axis=0),
np.percentile(simulated_paths, 95, axis=0),
color='lightblue', alpha=0.5, label='90%置信区间')
plt.plot(date_index, mean_path, 'b-', lw=2, label='模拟均值')
plt.plot(test_period.index, test_period.values, 'k-', lw=2.5, label='实际价格')
# 标记关键事件点
max_dev_idx = np.argmax(np.abs(test_period.values - mean_path[1:]))
event_date = test_period.index[max_dev_idx]
plt.axvline(x=event_date, color='purple', linestyle=':', alpha=0.8)
plt.text(event_date, plt.ylim()[0]*0.95, f'最大偏离点\n{event_date.strftime("%Y-%m-%d")}',
ha='center', fontsize=9)
plt.title('GBM模拟的90%置信区间与实际价格对比', fontsize=14)
plt.xlabel('日期')
plt.ylabel('价格')
plt.legend(loc='upper left')
plt.gca().xaxis.set_major_locator(mdates.MonthLocator(interval=2))
plt.gca().xaxis.set_major_formatter(mdates.DateFormatter('%Y-%m'))
plt.gcf().autofmt_xdate()
plt.grid(alpha=0.3)
plt.tight_layout()
plt.savefig('GBM_动态置信区间.png', dpi=300)
plt.show()
# 4. 计算预测误差指标
simulated_mean = mean_path[1:]
actual_prices = test_period.values
mae = np.mean(np.abs(simulated_mean - actual_prices))
rmse = np.sqrt(np.mean((simulated_mean - actual_prices)**2))
print("\n模型性能评估:")
print(f"平均绝对误差(MAE): {mae:.4f}")
print(f"均方根误差(RMSE): {rmse:.4f}")
print(f"年化波动率预测: {sigma:.4f} (实际: {test.std()*np.sqrt(252):.4f})")
# 5. 关键日期对比表
compare_dates = [test_period.index[0], test_period.index[len(test)//2], test_period.index[-1]]
compare_data = []
valid_dates = [d for d in compare_dates if d in date_index]
# valid_dates
for date in valid_dates:
idx = np.where(date_index == date)[0][0]
actual = df.loc[date, '收盘']
sim_mean = mean_path[idx]
sim_median = np.median(simulated_paths[:, idx])
compare_data.append([
date.strftime('%Y-%m-%d'),
actual,
sim_mean,
sim_median,
actual - sim_mean
])
# 创建对比表格
compare_df = pd.DataFrame(compare_data,
columns=['日期', '实际价格', '模拟均值', '模拟中位数', '偏差'])
print("\n关键日期价格对比:")
print(compare_df.to_string(index=False))
结果:
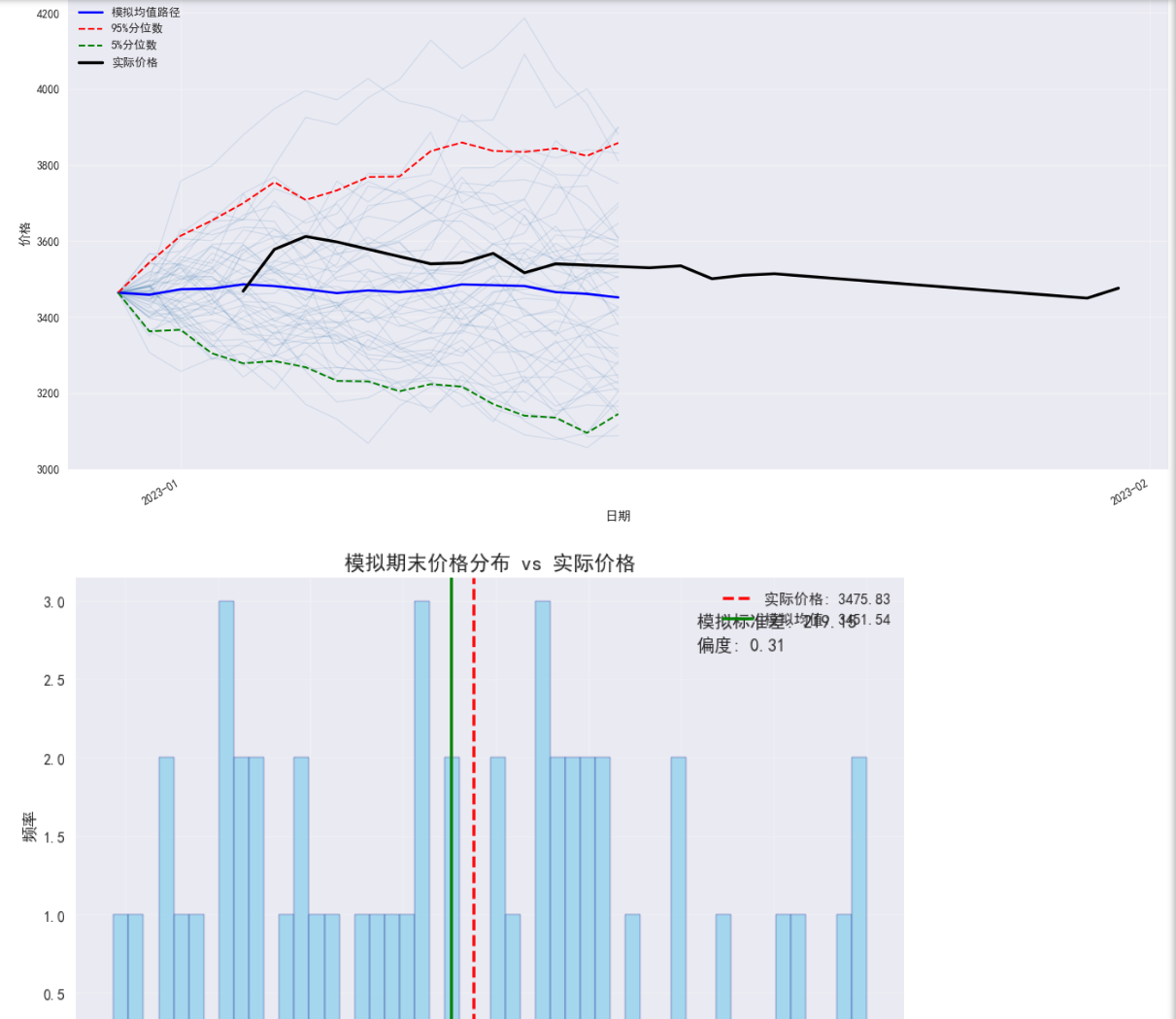
- 0
- 0
-
赞助
 支付宝
支付宝
 微信
微信
-
分享
