提示词

DataFrame以日期为索引，包含一列收盘价和一列对数收益，需要用可视化的方法研究其统计分布。我希望绘制一个1行2列的子图，第1列使用直方图展示对数收益的分布，第2列用QQ图展示对数收益的分布，请给出示例代码。

答案

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
import seaborn as sns

# 1. 创建示例数据（日期索引，收盘价和对数收益列）
df.columns = ['Close','Log_Return']

# 2. 创建1行2列的子图
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(14, 6))
fig.suptitle('股票对数收益率分布分析', fontsize=16, fontweight='bold')

# 3. 左侧子图：直方图 + KDE曲线[7,8,10](@ref)
ax1 = axes[0]
# 绘制直方图
sns.histplot(df['Log_Return'], bins=30, kde=False, 
             color='skyblue', edgecolor='white', 
             stat='density', alpha=0.7, ax=ax1)

# 添加KDE曲线[8](@ref)
sns.kdeplot(df['Log_Return'], color='darkred', lw=2, ax=ax1)

# 添加理论正态分布曲线
mu, std = df['Log_Return'].mean(), df['Log_Return'].std()
xmin, xmax = ax1.get_xlim()
x = np.linspace(xmin, xmax, 100)
p = stats.norm.pdf(x, mu, std)
ax1.plot(x, p, 'k--', linewidth=2, label='正态分布')

# 美化直方图
ax1.set_title('对数收益率分布直方图', fontsize=14)
ax1.set_xlabel('对数收益率', fontsize=12)
ax1.set_ylabel('密度', fontsize=12)
ax1.legend()
ax1.grid(alpha=0.2)

# 4. 右侧子图：QQ图（正态概率图）[1](@ref)
ax2 = axes[1]
# 创建QQ图
stats.probplot(df['Log_Return'].dropna(), dist="norm", plot=ax2)

# 添加参考线（完美正态分布）
ax2.get_lines()[1].set_color('red')  # 将参考线改为红色
ax2.get_lines()[1].set_linewidth(2)  # 加粗参考线

# 添加45度参考线
lims = np.array([ax2.get_xlim(), ax2.get_ylim()])
min_val = np.min(lims)
max_val = np.max(lims)
ax2.plot([min_val, max_val], [min_val, max_val], 'k--', alpha=0.5)

# 美化QQ图
ax2.set_title('QQ图（正态检验）', fontsize=14)
ax2.set_xlabel('理论分位数', fontsize=12)
ax2.set_ylabel('样本分位数', fontsize=12)
ax2.grid(alpha=0.2)

# 5. 添加统计指标注释
skewness = df['Log_Return'].skew()
kurtosis = df['Log_Return'].kurtosis()
jarque_bera = stats.jarque_bera(df['Log_Return'].dropna())

stats_text = (
    f"均值: {mu:.6f}\n"
    f"标准差: {std:.6f}\n"
    f"偏度: {skewness:.4f}\n"
    f"峰度: {kurtosis:.4f}\n"
    f"Jarque-Bera: {jarque_bera[0]:.2f}\n"
    f"p值: {jarque_bera[1]:.4f}"
)

fig.text(0.92, 0.75, stats_text, fontsize=11, 
         bbox=dict(boxstyle='round', facecolor='wheat', alpha=0.5),
         verticalalignment='top')

# 6. 调整布局并显示
plt.tight_layout(rect=[0, 0, 1, 0.96])  # 为总标题留出空间
plt.show()

# 7. 打印关键统计指标
print("对数收益率关键统计指标:")
print(f"样本大小: {len(df)}")
print(f"均值: {mu:.6f}")
print(f"标准差: {std:.6f}")
print(f"偏度: {skewness:.4f} ({'右偏' if skewness > 0 else '左偏'})")
print(f"峰度: {kurtosis:.4f} ({'尖峰' if kurtosis > 0 else '低峰'})")
print(f"Jarque-Bera正态性检验统计量: {jarque_bera[0]:.2f}, p值: {jarque_bera[1]:.4f}")
print(f"正态性结论: {'拒绝正态性假设' if jarque_bera[1] < 0.05 else '不能拒绝正态性假设'}")

数据导入以及防止画图中文乱码的代码是我加进去的，其余都是ai写的。

图像：

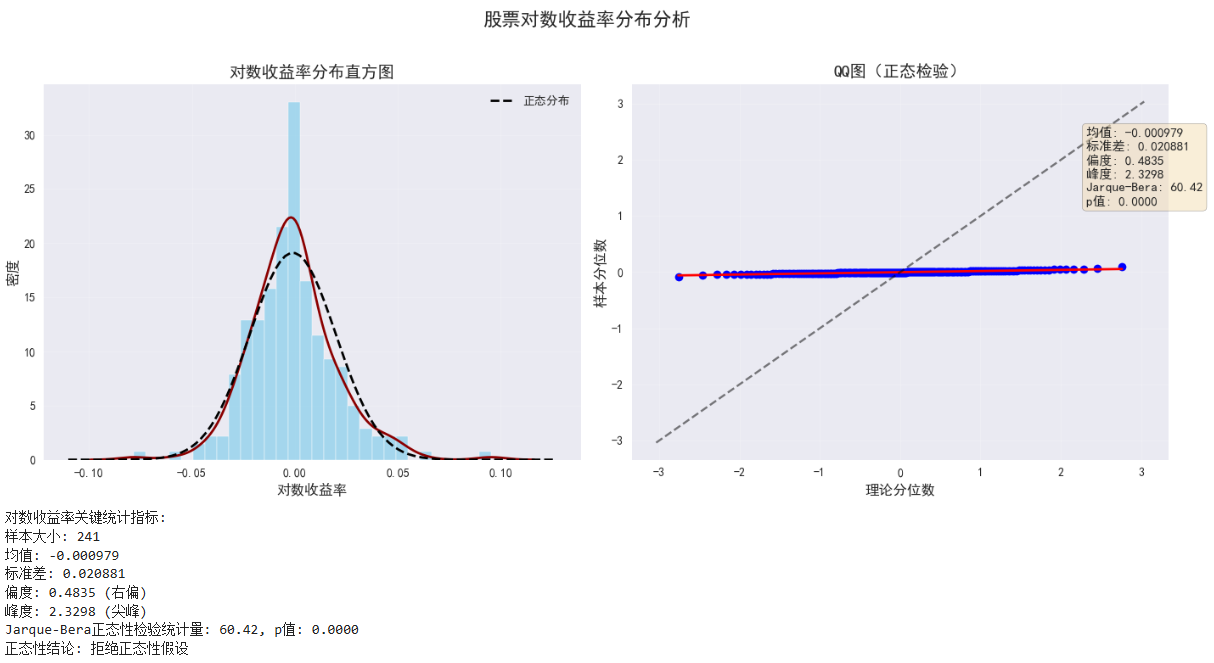
添加统计指标

前面ai实际已经给出了均值，不过我还想要输出中位数。

重新提示他

提示词

# Python代码
# 这里会用到scipy库，先将其导入
import scipy.stats as stats

# 创建一个1行2列的图形
fig, axes = plt.subplots(1, 2, dpi=300)

# 绘制对数收益的直方图
axes[0].hist(df['对数收益'], bins=20, color='blue', alpha=0.7)
axes[0].set_title('对数收益分布 - 直方图')

# 绘制对数收益的QQ图
stats.probplot(df['对数收益'], plot=axes[1])
axes[1].set_title('对数收益分布 - QQ图')

plt.tight_layout()
plt.savefig('图4-6.jpg', dpi=300)
plt.show()

现在我想输出DataFrame中对数收益的均值、中位数、标准差、峰度和偏度，请给出示例代码。

答案

import pandas as pd
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
from tabulate import tabulate  # 用于美化表格输出

# 1. 创建示例数据（日期索引，收盘价和对数收益列）
# np.random.seed(42)
# date_rng = pd.date_range(start='2024-01-01', periods=250, freq='D')
# prices = 100 + np.cumsum(np.random.normal(0.1, 0.5, 250))  # 模拟股价
# log_returns = np.log(prices[1:]/prices[:-1])  # 计算对数收益率

# df = pd.DataFrame({
#     'Close': prices[1:],  # 从第二天开始的价格
#     '对数收益': log_returns
# }, index=date_rng[1:])

# 2. 计算关键统计指标
stats_dict = {
    "均值": df['对数收益'].mean(),
    "中位数": df['对数收益'].median(),
    "标准差": df['对数收益'].std(),
    "偏度": df['对数收益'].skew(),  # 使用Pandas内置偏度计算
    "峰度": df['对数收益'].kurtosis()  # 使用Pandas内置峰度计算
}

# 使用Scipy验证计算结果（可选）
stats_dict_scipy = {
    "偏度(scipy)": stats.skew(df['对数收益'].dropna()),
    "峰度(scipy)": stats.kurtosis(df['对数收益'].dropna(), fisher=True)
}

# 3. 创建可视化图表（1行2列）
fig, axes = plt.subplots(1, 2, figsize=(14, 6), dpi=100)

# 直方图 + 密度曲线
sns.histplot(df['对数收益'], bins=25, kde=True, color='steelblue', ax=axes[0])
axes[0].axvline(stats_dict["均值"], color='red', linestyle='--', label=f'均值: {stats_dict["均值"]:.6f}')
axes[0].axvline(stats_dict["中位数"], color='green', linestyle='-.', label=f'中位数: {stats_dict["中位数"]:.6f}')
axes[0].set_title('对数收益率分布直方图', fontsize=14)
axes[0].set_xlabel('对数收益率', fontsize=12)
axes[0].set_ylabel('频率', fontsize=12)
axes[0].legend()
axes[0].grid(alpha=0.2)

# QQ图（正态概率图）
stats.probplot(df['对数收益'].dropna(), dist="norm", plot=axes[1])
axes[1].get_lines()[0].set_markerfacecolor('blue')  # 设置数据点颜色
axes[1].get_lines()[0].set_markersize(5.0)
axes[1].get_lines()[1].set_color('red')  # 设置参考线颜色
axes[1].set_title('对数收益率QQ图（正态检验）', fontsize=14)
axes[1].set_xlabel('理论分位数', fontsize=12)
axes[1].set_ylabel('样本分位数', fontsize=12)
axes[1].grid(alpha=0.2)

# 4. 添加统计信息文本框
stats_text = (
    f"均值: {stats_dict['均值']:.6f}\n"
    f"中位数: {stats_dict['中位数']:.6f}\n"
    f"标准差: {stats_dict['标准差']:.6f}\n"
    f"偏度: {stats_dict['偏度']:.4f}\n"
    f"峰度: {stats_dict['峰度']:.4f}"
)

fig.text(0.92, 0.25, stats_text, fontsize=12, 
         bbox=dict(boxstyle='round', facecolor='wheat', alpha=0.5),
         verticalalignment='top')

plt.tight_layout(rect=[0, 0, 0.85, 1])  # 为文本框留出空间
plt.savefig('log_returns_analysis.jpg', dpi=300)
plt.show()

# 5. 输出统计结果（表格形式）
stats_table = [
    ["统计指标", "值", "金融意义"],
    ["均值", f"{stats_dict['均值']:.6f}", "平均收益方向（正值为正收益）"],
    ["中位数", f"{stats_dict['中位数']:.6f}", "收益分布中心位置"],
    ["标准差", f"{stats_dict['标准差']:.6f}", "波动性/风险度量"],
    ["偏度", f"{stats_dict['偏度']:.4f}", 
     f"分布不对称性（>0 右偏，<0 左偏）\n当前: {'右偏' if stats_dict['偏度'] > 0 else '左偏'}"],
    ["峰度", f"{stats_dict['峰度']:.4f}", 
     f"尾部风险（>0 尖峰厚尾，<0 低峰薄尾）\n当前: {'尖峰厚尾' if stats_dict['峰度'] > 0 else '低峰薄尾'}"]
]

print("\n对数收益率描述性统计:")
print(tabulate(stats_table, headers="firstrow", tablefmt="fancy_grid"))

# 6. 输出正态性检验结果（Jarque-Bera检验）
jb_test = stats.jarque_bera(df['对数收益'].dropna())
print(f"\nJarque-Bera正态性检验:")
print(f"统计量: {jb_test[0]:.4f}, p值: {jb_test[1]:.4f}")
print("结论: " + ("拒绝正态性假设（非正态分布）" if jb_test[1] < 0.05 else "不能拒绝正态性假设"))

图像：

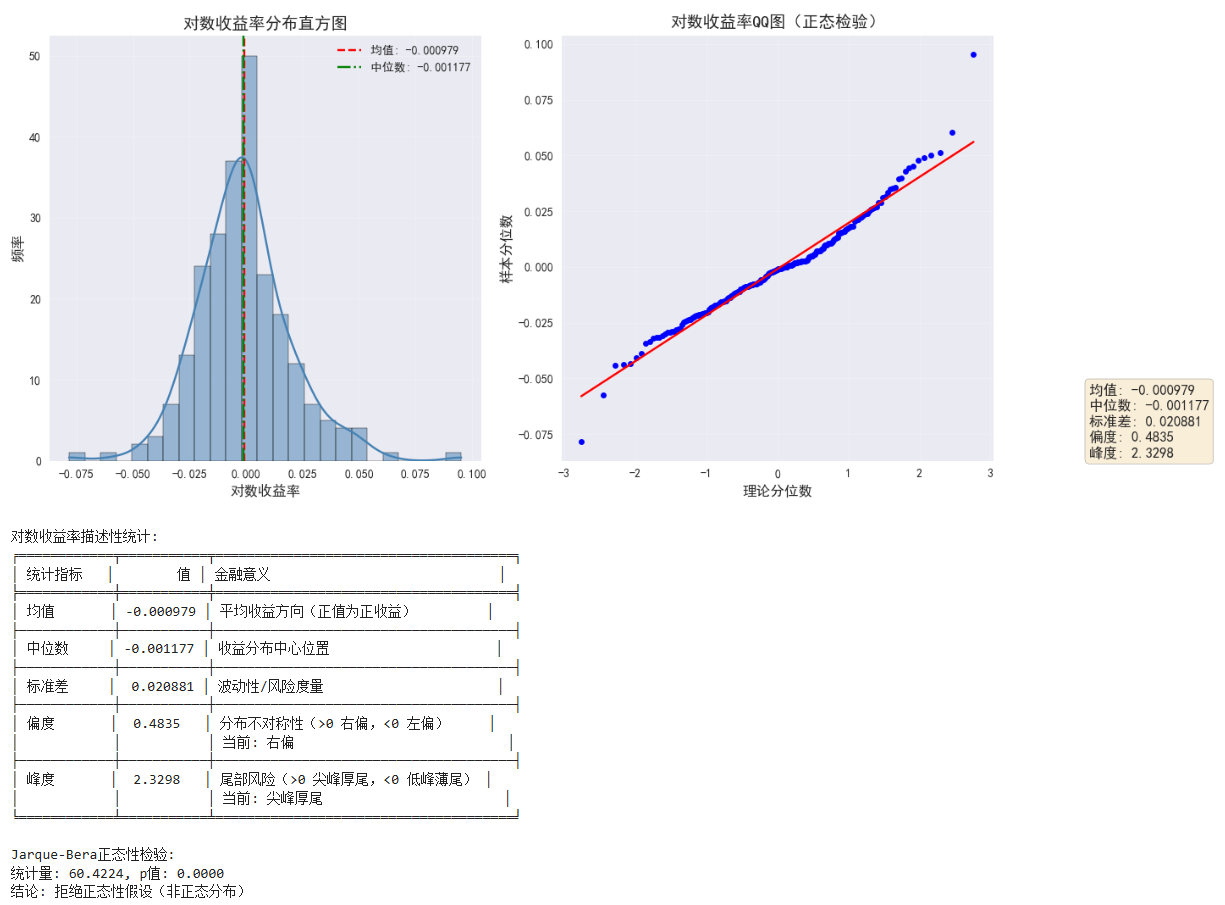
在 Pandas 的 .kurtosis() 方法中，默认使用 Fisher 的定义（减 3 处理），使得正态分布的峰度为 0。