提示词

请用包含3行1列子图的图形来展示资产回报的杠杆效应，要求第一行子图是DataFrame中的收盘价，第二行是对数收益，第三行子图是对数收益的20日滚动标准差和30日滚动标准差。

答案

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import PercentFormatter

# 1. 创建示例数据（日期索引，收盘价）
# np.random.seed(42)
# date_rng = pd.date_range(start='2024-01-01', periods=250, freq='D')
# prices = 100 + np.cumsum(np.random.normal(0.1, 0.5, 250))  # 模拟股价序列
# df = pd.DataFrame({'Close': prices}, index=date_rng)

# 2. 计算对数收益率
# df['Log_Return'] = np.log(df['Close'] / df['Close'].shift(1))  # [9,11](@ref)

# 3. 计算滚动标准差
df['Rolling_Std_20'] = df['对数收益'].rolling(window=20).std() * np.sqrt(252)  # 年化波动率 [12,13](@ref)
df['Rolling_Std_30'] = df['对数收益'].rolling(window=30).std() * np.sqrt(252)

# 4. 创建图形布局
plt.figure(figsize=(14, 12))
plt.rcParams['font.sans-serif'] = ['SimHei']  # 中文显示
plt.rcParams['axes.unicode_minus'] = False

fig, (ax1, ax2, ax3) = plt.subplots(3, 1, dpi=300, sharex=True)

# 第一子图：收盘价
# ax1 = plt.subplot(3, 1, 1)
ax1.plot(df['收盘'], color='darkblue', linewidth=1.5)
ax1.set_title('资产价格走势', fontsize=14, pad=20)
ax1.set_ylabel('收盘价', fontsize=12)
ax1.grid(alpha=0.3)
# ax1.fill_between(df.index, df['收盘'], alpha=0.2, color='skyblue')  # 增强可视化

# 第二子图：对数收益率
# ax2 = plt.subplot(3, 1, 2)
ax2.bar(df.index, df['对数收益']*100, color=np.where(df['对数收益']>0, 'forestgreen', 'firebrick'), alpha=0.7, width=1)
ax2.set_title('日度对数收益率', fontsize=14, pad=15)
ax2.set_ylabel('收益率 (%)', fontsize=12)
ax2.yaxis.set_major_formatter(PercentFormatter(decimals=1))  # 百分比格式 [10](@ref)
ax2.grid(alpha=0.3)
ax2.set_ylim([-8, 8])  # 统一Y轴范围

# 第三子图：滚动标准差
# ax3 = plt.subplot(3, 1, 3)
ax3.plot(df['Rolling_Std_20'], label='20日波动率', color='darkorange', linewidth=1.5)
ax3.plot(df['Rolling_Std_30'], label='30日波动率', color='purple', linewidth=1.5, linestyle='--')
ax3.set_title('波动率趋势（年化标准差）', fontsize=14, pad=15)
ax3.set_ylabel('波动率 (%)', fontsize=12)
ax3.set_xlabel('日期', fontsize=12)
ax3.legend(loc='upper right', framealpha=0.9)
ax3.grid(alpha=0.3)
ax3.set_ylim(bottom=0)  # 波动率非负

# 调整布局
plt.tight_layout(h_pad=3)  # 子图间距优化
plt.savefig('leverage_effect_analysis.jpg', dpi=300, bbox_inches='tight')
plt.show()

我增加了共享1个x轴的代码，其余都是ai写的。

图像：

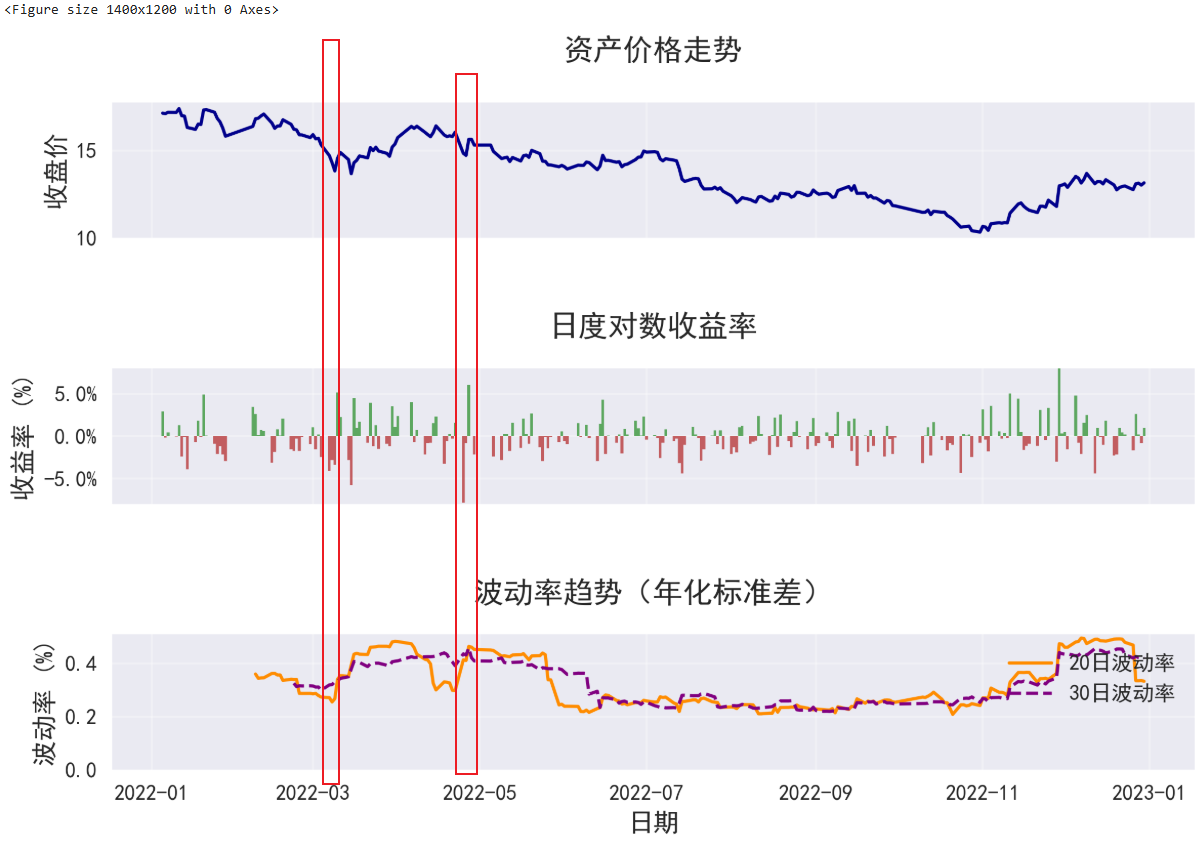
标记红框，可以看到，在大部分时间里，当价格下跌之后，波动性增加；而当价格上升之后，波动性减小。