提示词

现在有3个DataFrame，第一个名为tesla_monthly，其中Adj Close列存储了特斯拉月度收盘价，第二个名为factors，是月度三因子数据，包括的列为Mkt-RF、SMB、HML和RF，第三个名为mom_df，是月度动量因子，需要使用这三个DataFrame演示Carhart四因子模型，请给出示例代码。

答案

import pandas as pd
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib.ticker import PercentFormatter

# 1. 数据准备与预处理
# 假设已有三个DataFrame:
#   tesla_monthly: 包含日期索引和'Adj Close'列
#   factors: 包含日期索引和列['Mkt-RF','SMB','HML','RF']
#   mom_df: 包含日期索引和动量因子数据

# 1.1 计算特斯拉月度收益率
tesla_returns = tesla_monthly['Adj Close'].pct_change().dropna()
tesla_returns.name = 'TSLA_Return'

# 1.2 合并所有因子数据
# 确保所有数据频率相同（月度）
carhart_data = pd.concat([
    tesla_returns, 
    factors,
    mom_df
], axis=1).dropna()

# 1.3 计算特斯拉超额收益
carhart_data['TSLA_Excess'] = carhart_data['TSLA_Return'] - carhart_data['RF']

# 1.4 确认因子列名
# 假设动量因子列名为'MOM'
print("数据包含的列:", carhart_data.columns.tolist())
print("\n前5行数据示例:")
print(carhart_data.head())

# 2. Carhart四因子模型回归
def run_carhart_regression(data):
    """执行Carhart四因子回归"""
    X = data[['Mkt-RF', 'SMB', 'HML', 'Mom']]
    X = sm.add_constant(X)  # 添加截距项
    y = data['TSLA_Excess']
  
    model = sm.OLS(y, X).fit(cov_type='HAC', cov_kwds={'maxlags': 3})
    return model

# 全样本回归
full_model = run_carhart_regression(carhart_data)

# 3. 滚动估计（36个月窗口）
WINDOW_SIZE = 36  # 3年滚动窗口
dates = []
alphas = []
betas_mkt = []
betas_smb = []
betas_hml = []
betas_mom = []
r_squared = []
pvalues_alpha = []

print("\n开始滚动四因子模型估计...")
for i in range(WINDOW_SIZE, len(carhart_data)):
    window_data = carhart_data.iloc[i-WINDOW_SIZE:i]
    model = run_carhart_regression(window_data)
  
    # 存储结果
    dates.append(carhart_data.index[i])
    alphas.append(model.params['const'])
    betas_mkt.append(model.params['Mkt-RF'])
    betas_smb.append(model.params['SMB'])
    betas_hml.append(model.params['HML'])
    betas_mom.append(model.params['Mom'])
    r_squared.append(model.rsquared)
    pvalues_alpha.append(model.pvalues['const'])

# 创建结果DataFrame
results = pd.DataFrame({
    'Date': dates,
    'Alpha': alphas,
    'Beta_Mkt': betas_mkt,
    'Beta_SMB': betas_smb,
    'Beta_HML': betas_hml,
    'Beta_MOM': betas_mom,
    'R_squared': r_squared,
    'Alpha_Pvalue': pvalues_alpha
}).set_index('Date')

# 4. 可视化分析
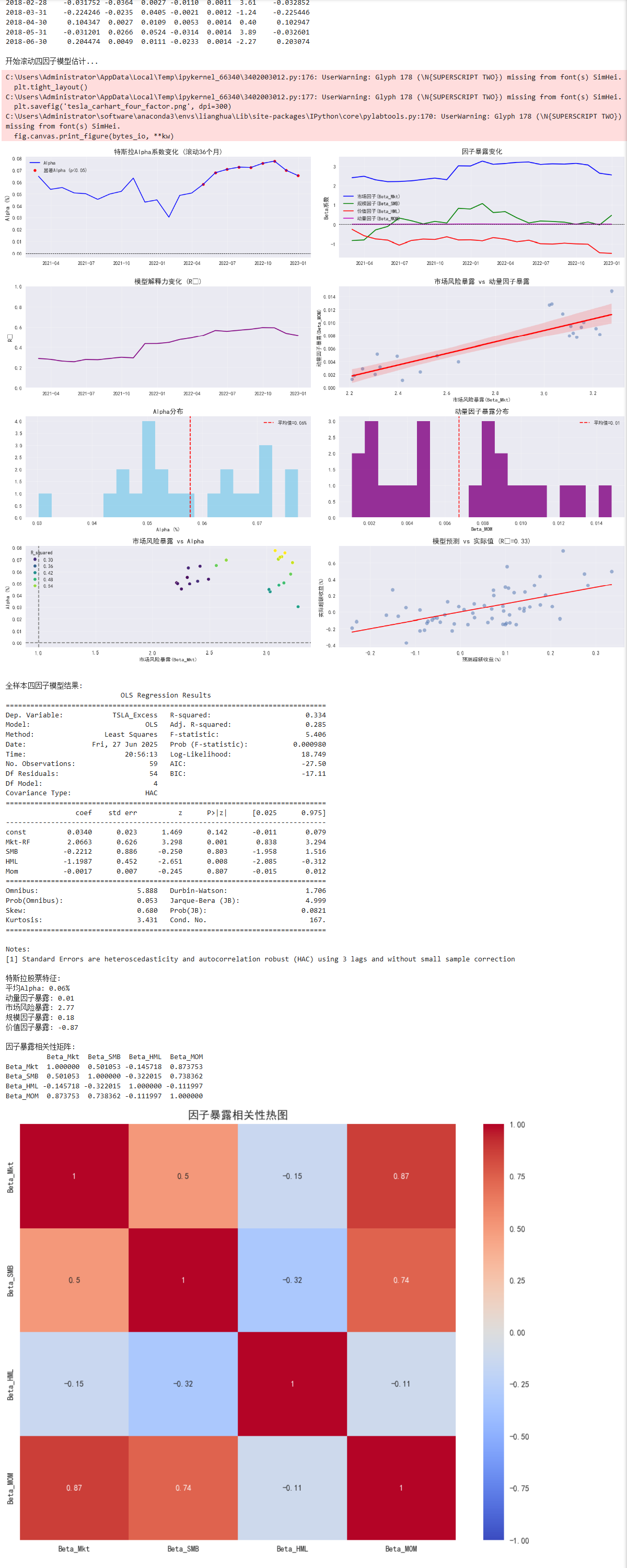
plt.figure(figsize=(18, 15))

# 4.1 Alpha系数变化 (标记统计显著性)
plt.subplot(4, 2, 1)
plt.plot(results.index, results['Alpha'], 'b-', lw=1.5, label='Alpha')

# 标记显著的Alpha点（p<0.05）
significant_dates = results[results['Alpha_Pvalue'] < 0.05].index
significant_alphas = results.loc[significant_dates, 'Alpha']
plt.scatter(significant_dates, significant_alphas, 
            color='red', s=30, label='显著Alpha (p<0.05)')

plt.axhline(0, color='black', linestyle='--', lw=0.8)
plt.title('特斯拉Alpha系数变化 (滚动36个月)', fontsize=14)
plt.ylabel('Alpha (%)', fontsize=12)
plt.legend()
plt.grid(alpha=0.3)

# 4.2 因子暴露变化
plt.subplot(4, 2, 2)
plt.plot(results.index, results['Beta_Mkt'], 'b-', label='市场因子(Beta_Mkt)')
plt.plot(results.index, results['Beta_SMB'], 'g-', label='规模因子(Beta_SMB)')
plt.plot(results.index, results['Beta_HML'], 'r-', label='价值因子(Beta_HML)')
plt.plot(results.index, results['Beta_MOM'], 'm-', label='动量因子(Beta_MOM)')
plt.axhline(0, color='black', linestyle='--', lw=0.8)
plt.title('因子暴露变化', fontsize=14)
plt.ylabel('Beta系数', fontsize=12)
plt.legend(loc='best')
plt.grid(alpha=0.3)

# 4.3 R²变化
plt.subplot(4, 2, 3)
plt.plot(results.index, results['R_squared'], 'purple')
plt.title('模型解释力变化 (R²)', fontsize=14)
plt.ylabel('R²', fontsize=12)
plt.ylim(0, 1)
plt.grid(alpha=0.3)

# 4.4 Beta_Mkt与Beta_MOM关系
plt.subplot(4, 2, 4)
sns.regplot(x=results['Beta_Mkt'], y=results['Beta_MOM'], 
            scatter_kws={'alpha':0.5}, line_kws={'color':'red'})
plt.title('市场风险暴露 vs 动量因子暴露', fontsize=14)
plt.xlabel('市场风险暴露(Beta_Mkt)')
plt.ylabel('动量因子暴露(Beta_MOM)')
plt.grid(alpha=0.3)

# 4.5 Alpha分布直方图
plt.subplot(4, 2, 5)
plt.hist(results['Alpha'], bins=20, color='skyblue', alpha=0.8)
plt.axvline(results['Alpha'].mean(), color='r', linestyle='--', 
            label=f'平均值={results["Alpha"].mean():.2f}%')
plt.title('Alpha分布', fontsize=14)
plt.xlabel('Alpha (%)')
plt.legend()
plt.grid(alpha=0.3)

# 4.6 动量因子暴露分布
plt.subplot(4, 2, 6)
plt.hist(results['Beta_MOM'], bins=20, color='purple', alpha=0.8)
plt.axvline(results['Beta_MOM'].mean(), color='r', linestyle='--',
            label=f'平均值={results["Beta_MOM"].mean():.2f}')
plt.title('动量因子暴露分布', fontsize=14)
plt.xlabel('Beta_MOM')
plt.legend()
plt.grid(alpha=0.3)

# 4.7 市场风险暴露 vs Alpha
plt.subplot(4, 2, 7)
sns.scatterplot(x=results['Beta_Mkt'], y=results['Alpha'], 
                hue=results['R_squared'], palette='viridis')
plt.axhline(0, color='grey', linestyle='--')
plt.axvline(1, color='grey', linestyle='--')
plt.title('市场风险暴露 vs Alpha', fontsize=14)
plt.xlabel('市场风险暴露(Beta_Mkt)')
plt.ylabel('Alpha (%)')
plt.grid(alpha=0.3)

# 4.8 最终模型预测vs实际值
plt.subplot(4, 2, 8)
plt.scatter(full_model.fittedvalues, carhart_data['TSLA_Excess'], alpha=0.5)
plt.plot([min(full_model.fittedvalues), max(full_model.fittedvalues)], 
         [min(full_model.fittedvalues), max(full_model.fittedvalues)], 
         color='red')
plt.title(f'模型预测 vs 实际值 (R²={full_model.rsquared:.2f})', fontsize=14)
plt.xlabel('预测超额收益(%)')
plt.ylabel('实际超额收益(%)')
plt.grid(alpha=0.3)

plt.tight_layout()
plt.savefig('tesla_carhart_four_factor.png', dpi=300)
plt.show()

# 5. 输出结果分析
print("\n全样本四因子模型结果:")
print(full_model.summary())

# 6. 投资策略分析
avg_alpha = results['Alpha'].mean()
avg_mom_beta = results['Beta_MOM'].mean()

print("\n特斯拉股票特征:")
print(f"平均Alpha: {avg_alpha:.2f}%")
print(f"动量因子暴露: {avg_mom_beta:.2f}")
print(f"市场风险暴露: {results['Beta_Mkt'].mean():.2f}")
print(f"规模因子暴露: {results['Beta_SMB'].mean():.2f}")
print(f"价值因子暴露: {results['Beta_HML'].mean():.2f}")

# 7. 因子暴露相关性分析
beta_corr = results[['Beta_Mkt', 'Beta_SMB', 'Beta_HML', 'Beta_MOM']].corr()
print("\n因子暴露相关性矩阵:")
print(beta_corr)

# 可视化相关性矩阵
plt.figure(figsize=(10, 8))
sns.heatmap(beta_corr, annot=True, cmap='coolwarm', vmin=-1, vmax=1)
plt.title('因子暴露相关性热图', fontsize=14)
plt.tight_layout()
plt.show()

结果：